题目内容
在数列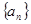
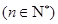 中,其前
中,其前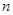 项和为
项和为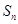 ,满足
,满足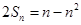 .
.
(1)求数列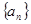 的通项公式;
的通项公式;
(2)设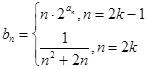 (
(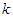 为正整数),求数列
为正整数),求数列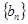 的前
的前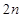 项和
项和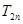 .
.
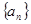
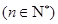 中,其前
中,其前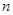 项和为
项和为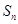 ,满足
,满足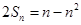 .
.(1)求数列
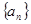 的通项公式;
的通项公式;(2)设
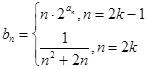 (
(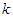 为正整数),求数列
为正整数),求数列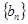 的前
的前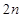 项和
项和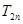 .
.(1) 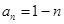 .(2)
.(2)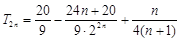 .
.
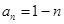 .(2)
.(2)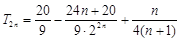 .
.试题分析:(1)根据
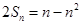 ,计算
,计算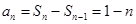
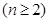
验证当
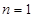 时,
时,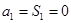 ,明确数列
,明确数列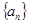 是
是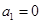 为首项、公差为
为首项、公差为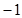 的等差数列即得所求.
的等差数列即得所求.(2)由(1)知:
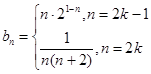
利用“裂项相消法”、“错位相减法”求和.
试题解析:(1)由题设得:
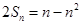 ,所以
,所以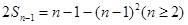
所以
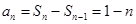
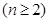 2分
2分当
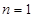 时,
时,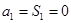 ,数列
,数列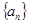 是
是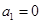 为首项、公差为
为首项、公差为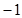 的等差数列
的等差数列故
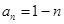 . 5分
. 5分(2)由(1)知:
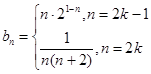 6分
6分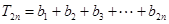
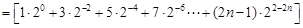
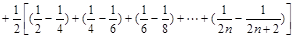
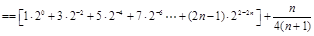 9分
9分设
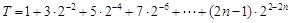
则
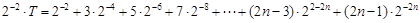
两式相减得:
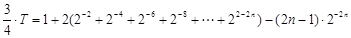
整理得:
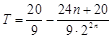 11分
11分所以
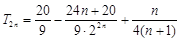 12分
12分
练习册系列答案
 教学练新同步练习系列答案
教学练新同步练习系列答案 课前课后同步练习系列答案
课前课后同步练习系列答案 课堂小作业系列答案
课堂小作业系列答案 黄冈小状元口算速算练习册系列答案
黄冈小状元口算速算练习册系列答案 成功训练计划系列答案
成功训练计划系列答案
相关题目
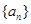 是公比大于
是公比大于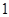 的等比数列,
的等比数列,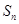 为数列
为数列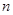 项和.已知
项和.已知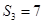 ,且
,且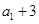 ,
,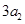 ,
,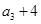 构成等差数列.
构成等差数列.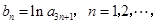 求数列
求数列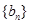 的前
的前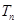 .
.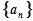 的前
的前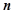 项和为
项和为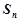 ,
,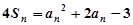 ,若
,若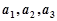 成等比数列,且
成等比数列,且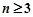 时,
时,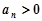 .
.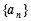 成等差数列;
成等差数列;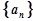 的前n项和
的前n项和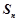 .
.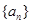 ,若点
,若点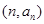
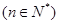 均在直线
均在直线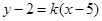 上,则数列
上,则数列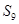 等于( )
等于( )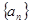 的前
的前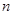 项和为
项和为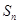 ,若
,若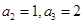 ,则
,则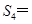
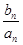 的最大值和最小值;
的最大值和最小值; 求a1+a2+a3+a4+…+a99+a100的值.
求a1+a2+a3+a4+…+a99+a100的值.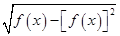 +
+ 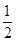 ,设an=[f(n)]2-f(n),数列{an}的前15项的和为
,设an=[f(n)]2-f(n),数列{an}的前15项的和为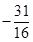 ,则f(15)= .
,则f(15)= .