题目内容
已知数列an=n-16,bn=(-1)n|n-15|,其中n∈N*.
(1)求满足an+1=|bn|的所有正整数n的集合;
(2)若n≠16,求数列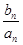 的最大值和最小值;
的最大值和最小值;
(3)记数列{anbn}的前n项和为Sn,求所有满足S2m=S2n(m<n)的有序整数对(m,n).
(1)求满足an+1=|bn|的所有正整数n的集合;
(2)若n≠16,求数列
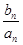 的最大值和最小值;
的最大值和最小值;(3)记数列{anbn}的前n项和为Sn,求所有满足S2m=S2n(m<n)的有序整数对(m,n).
(1){n|n≥15,n∈N*}(2)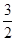 (n=18),最小值-2(n=17)(3)S16=S14,m=7,n=8
(n=18),最小值-2(n=17)(3)S16=S14,m=7,n=8
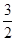 (n=18),最小值-2(n=17)(3)S16=S14,m=7,n=8
(n=18),最小值-2(n=17)(3)S16=S14,m=7,n=8(1)an+1=|bn|,n-15=|n-15|.
当n≥15时,an+1=|bn|恒成立;
当n<15时,n-15=-(n-15),n=15(舍去).
∴n的集合为{n|n≥15,n∈N*}.
(2)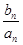 =
=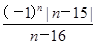 .
.
(ⅰ)当n>16时,n取偶数时,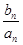 =
=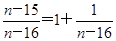 ,
,
当n=18时,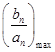 =
=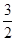 ,无最小值;n取奇数时,
,无最小值;n取奇数时,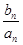 =-1-
=-1-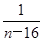 ,
,
n=17时,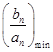 =-2,无最大值.
=-2,无最大值.
(ⅱ)当n<16时,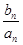 =
=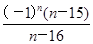 .
.
当n为偶数时,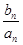 =
=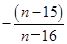 =-1-
=-1-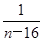 .
.
n=14时,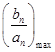 =-
=-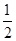 ,
,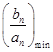 =-
=-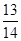 ;
;
当n为奇数时,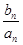 =
=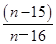 =1+
=1+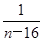 ,
,
n=1时,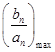 =1-
=1-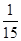 =
=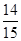 ,n=15时,
,n=15时,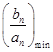 =0.
=0.
综上,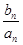 最大值为
最大值为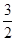 (n=18),最小值-2(n=17).
(n=18),最小值-2(n=17).
(3)当n≤15时,bn=(-1)n-1(n-15),a2k-1b2k-1+a2kb2k=2(16-2k)≥0,
当n>15时,bn=(-1)n(n-15),a2k-1b2k-1+a2kb2k=2(2k-16)>0,其中a15b15+a16b16=0,
∴S16=S14,m=7,n=8.
当n≥15时,an+1=|bn|恒成立;
当n<15时,n-15=-(n-15),n=15(舍去).
∴n的集合为{n|n≥15,n∈N*}.
(2)
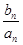 =
=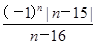 .
.(ⅰ)当n>16时,n取偶数时,
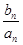 =
=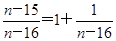 ,
,当n=18时,
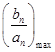 =
=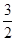 ,无最小值;n取奇数时,
,无最小值;n取奇数时,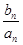 =-1-
=-1-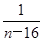 ,
,n=17时,
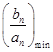 =-2,无最大值.
=-2,无最大值.(ⅱ)当n<16时,
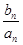 =
=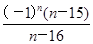 .
.当n为偶数时,
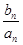 =
=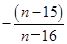 =-1-
=-1-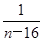 .
.n=14时,
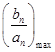 =-
=-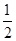 ,
,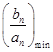 =-
=-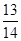 ;
;当n为奇数时,
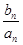 =
=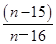 =1+
=1+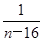 ,
,n=1时,
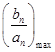 =1-
=1-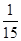 =
=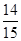 ,n=15时,
,n=15时,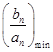 =0.
=0.综上,
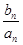 最大值为
最大值为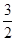 (n=18),最小值-2(n=17).
(n=18),最小值-2(n=17).(3)当n≤15时,bn=(-1)n-1(n-15),a2k-1b2k-1+a2kb2k=2(16-2k)≥0,
当n>15时,bn=(-1)n(n-15),a2k-1b2k-1+a2kb2k=2(2k-16)>0,其中a15b15+a16b16=0,
∴S16=S14,m=7,n=8.

练习册系列答案
相关题目
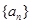 前
前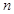 项和为
项和为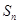 ,向量
,向量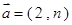 与
与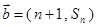 ,且
,且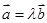 ,
,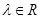
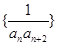 的前
的前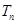 ,不等式
,不等式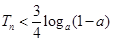 对任意的正整数
对任意的正整数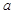 的取值范围.
的取值范围.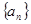
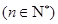 中,其前
中,其前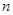 项和为
项和为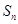 ,满足
,满足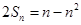 .
.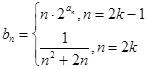 (
(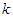 为正整数),求数列
为正整数),求数列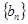 的前
的前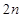 项和
项和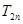 .
.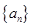 中,若
中,若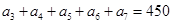 ,则
,则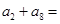 ( )
( )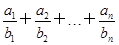 (n∈N*),若Tn+
(n∈N*),若Tn+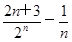 <c(c∈Z)恒成立,求c的最小值.
<c(c∈Z)恒成立,求c的最小值.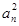 -(2n-1)an-2n=0.
-(2n-1)an-2n=0.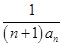 ,求数列{bn}的前n项和Tn.
,求数列{bn}的前n项和Tn.