题目内容
12.已知函数f(x)=$\sqrt{2}$sin(2x+$\frac{π}{4}$),则f(x)在x∈[0,$\frac{π}{2}$]时的值域是[-1,$\sqrt{2}$];又若将函数y=f(x)的图象向左平移a(a>0)个单位长度得到的图象恰好关于点($\frac{π}{4}$,0)对称,则实数a的最小值为$\frac{π}{8}$.分析 由x∈[0,$\frac{π}{2}$]可解得$\frac{π}{4}$≤2x+$\frac{π}{4}$≤$\frac{5π}{4}$,根据正弦函数的性质即可求得f(x)在x∈[0,$\frac{π}{2}$]时的值域;
由题意可得:f(x)=$\sqrt{2}$sin(2x+$\frac{π}{4}$),平移a个单位长度后得到函数f(x)=$\sqrt{2}$sin(2x+2a+$\frac{π}{4}$),根据对称性可得2×$\frac{π}{4}$+2a+$\frac{π}{4}$=kπ(k∈Z),即可得到a=-$\frac{3π}{8}$+$\frac{kπ}{2}$,(k∈Z)进而得到答案.
解答 解:∵x∈[0,$\frac{π}{2}$],
∴$\frac{π}{4}$≤2x+$\frac{π}{4}$≤$\frac{5π}{4}$,
根据正弦函数的性质得,sin(2x+$\frac{π}{4}$)∈[-$\frac{\sqrt{2}}{2}$,1],则$\sqrt{2}$sin(2x+$\frac{π}{4}$)∈[-1,$\sqrt{2}$],
∴f(x)的值域是[-1,$\sqrt{2}$].
将函数y=f(x)的图象向左平移a(a>0)个单位长度得到函数f(x)=$\sqrt{2}$sin(2(x+a)+$\frac{π}{4}$)=$\sqrt{2}$sin(2x+2a+$\frac{π}{4}$)的图象,
∵函数y=$\sqrt{2}$sin(2x+2a+$\frac{π}{4}$)关于点($\frac{π}{4}$,0)对称,
所以2×$\frac{π}{4}$+2a+$\frac{π}{4}$=kπ(k∈Z),即a=-$\frac{3π}{8}$+$\frac{kπ}{2}$,(k∈Z)
因为a>0,所以k>$\frac{3}{4}$
所以当k=1时,a有最小值$\frac{π}{8}$.
故答案为:[-1,$\sqrt{2}$],$\frac{π}{8}$
点评 本题主要考查正弦函数的有关性质,即对称性、单调性以及三角函数图象的平移变换,属于中档题.


| A. | f(x)=sinx | B. | f(x)=|x| | C. | f(x)=$\frac{1}{2}$(2x+2-x) | D. | f(x)=ln$\frac{2-x}{2+x}$ |
 如图,网格纸上小止方形的边长为1,粗实线画出的是某多面体的三视图,则该多面体的体积为( )
如图,网格纸上小止方形的边长为1,粗实线画出的是某多面体的三视图,则该多面体的体积为( )| A. | 16 | B. | 20 | C. | 4$\sqrt{29}$ | D. | 60 |
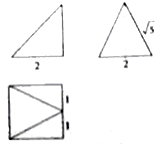
| A. | 4$\sqrt{5}$ | B. | $\frac{4\sqrt{5}}{3}$ | C. | $\frac{8}{3}$ | D. | $\frac{4}{3}$ |
| A. | x2=$\frac{1}{2}$y | B. | x2=y | C. | x2=2y | D. | x2=4y |