题目内容
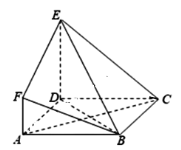
【题目】四面体ABCD的每个顶点都在球O的表面上,AB是球O的一条直径,且AC=2,BC=4,现有下面四个结论:
①球O的表面积为20π;②AC上存在一点M,使得AD∥BM;
③若AD=3,则BD=4;④四面体ABCD体积的最大值为![]() .
.
其中所有正确结论的编号是( )
A.①②B.②④C.①④D.①③④
【答案】C
【解析】
由AC=2,BC=4可求得直径为AB=2![]() ,从而可判断①③;由AD与平面ABC相交可判断②;由D到平面ABC的距离的最大值为球的半径可判断④.
,从而可判断①③;由AD与平面ABC相交可判断②;由D到平面ABC的距离的最大值为球的半径可判断④.
因为AB是球O的一条直径,所以AC⊥BC,AD⊥BD,所以AB=2![]() .
.
若AD=3,则BD=![]() ,③错;
,③错;
球的半径为![]() ,球O的表面积为4π×(
,球O的表面积为4π×(![]() )2=20π ,①对;
)2=20π ,①对;
因为AD与平面ABC相交,所以AC上找不到一点M,使得AD∥BM.,②错;
因为D到平面ABC的距离的最大值为球的半径,所以四面体ABCD体积的最大值为
![]() ×
×![]() ×2×4×
×2×4×![]() =
=![]() .④对,
.④对,
即所有正确结论的编号是①④.
故选:C.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案【题目】某企业新研发了一种产品,产品的成本由原料成本及非原料成本组成.每件产品的非原料成本![]() (元)与生产该产品的数量
(元)与生产该产品的数量![]() (千件)有关,经统计得到如下数据:
(千件)有关,经统计得到如下数据:
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 112 | 61 | 44.5 | 35 | 30.5 | 28 | 25 | 24 |
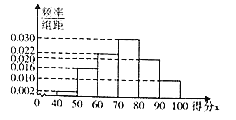
根据以上数据,绘制了散点图.
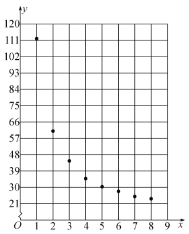
观察散点图,两个变量不具有线性相关关系,现考虑用反比例函数模型![]() 和指数函数模型
和指数函数模型![]() 分别对两个变量的关系进行拟合.已求得用指数函数模型拟合的回归方程为
分别对两个变量的关系进行拟合.已求得用指数函数模型拟合的回归方程为![]() ,
,![]() 与
与![]() 的相关系数
的相关系数![]() .
.
参考数据(其中![]() ):
):
|
|
|
|
|
|
|
|
183.4 | 0.34 | 0.115 | 1.53 | 360 | 22385.5 | 61.4 | 0.135 |
(1)用反比例函数模型求![]() 关于
关于![]() 的回归方程;
的回归方程;
(2)用相关系数判断上述两个模型哪一个拟合效果更好(精确到0.01),并用其估计产量为10千件时每件产品的非原料成本;
(3)该企业采取订单生产模式(根据订单数量进行生产,即产品全部售出).根据市场调研数据,若该产品单价定为100元,则签订9千件订单的概率为0.8,签订10千件订单的概率为0.2;若单价定为90元,则签订10千件订单的概率为0.3,签订11千件订单的概率为0.7.已知每件产品的原料成本为10元,根据(2)的结果,企业要想获得更高利润,产品单价应选择100元还是90元,请说明理由.
参考公式:对于一组数据![]() ,
,![]() ,…,
,…,![]() ,其回归直线
,其回归直线![]() 的斜率和截距的最小二乘估计分别为:
的斜率和截距的最小二乘估计分别为: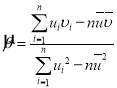 ,
,![]() ,相关系数
,相关系数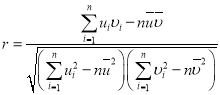 .
.