题目内容
【题目】如图,在三棱柱![]() 中,已知
中,已知![]() 侧面
侧面![]() ,
,![]() ,
,![]() ,
,![]() ,点
,点![]() 在棱
在棱![]() 上.
上.
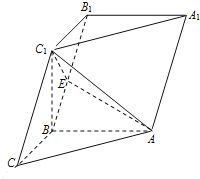
(Ⅰ)求证:![]() 平面
平面![]() ;
;
(Ⅱ)试确定点![]() 的位置,使得二面角
的位置,使得二面角![]() 的余弦值为
的余弦值为![]() .
.
【答案】(Ⅰ)详见解析;(Ⅱ)点![]() 在
在![]() 的中点.
的中点.
【解析】
试题分析:(Ⅰ)首先根据余弦定理计算![]() ,在
,在![]() 中满足勾股定理,
中满足勾股定理,![]() ,然后根据题设所给的
,然后根据题设所给的![]() 平面
平面![]() ,得到
,得到![]() ,这样就证明了线面垂直的条件;
,这样就证明了线面垂直的条件;
(Ⅱ)由(Ⅰ)知,BC、BA、BC1两两垂直,以B为空间坐标系的原点,建立如图所示的坐标系,设![]() ,这样设点的坐标,求平面
,这样设点的坐标,求平面![]() 和平面
和平面![]() 的法向量
的法向量![]() ,根据
,根据![]() 求
求![]() ,确定点E的位置.
,确定点E的位置.
试题解析:解:(Ⅰ)证明:∵BC=![]() ,CC1=BB1=2,∠BCC1=
,CC1=BB1=2,∠BCC1=![]() ,在△BCC1中,由余弦定理,可求得C1B=
,在△BCC1中,由余弦定理,可求得C1B=![]() ,
,
∴C1B2+BC2=![]() ,即C1B⊥BC.
,即C1B⊥BC.
又AB⊥侧面BCC1B1,故AB⊥BC1,又CB∩AB=B,所以C1B⊥平面ABC;
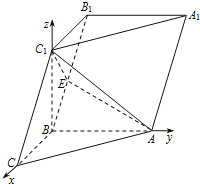
(Ⅱ)解:由(Ⅰ)知,BC、BA、BC1两两垂直,以B为空间坐标系的原点,建立如图所示的坐标系,
则B(0,0,0),A(0,2,0),C(![]() ,0,0),C1(0,0,
,0,0),C1(0,0,![]() ),B1(﹣
),B1(﹣![]() ,0,
,0,![]() ),
),
∴![]() =(0,2,﹣
=(0,2,﹣![]() ),
),
设![]() ,则
,则![]() =
=![]() +λ
+λ![]() =(0,0,﹣
=(0,0,﹣![]() )+λ(﹣
)+λ(﹣![]() ,0,
,0,![]() )=(﹣
)=(﹣![]() λ,0,﹣
λ,0,﹣![]() +
+![]() λ)
λ)
设平面AC1E的一个法向量为![]() =(x,y,z),由
=(x,y,z),由![]() ,得
,得![]() ,
,
令z=![]() ,取
,取![]() =(
=(![]() ,1,
,1,![]() ),
),
又平面C1EC的一个法向量为![]() =(0,1,0)
=(0,1,0)
所以cos<![]() ,
,![]() >=
>=![]() =
=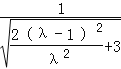 =
=![]() ,解得λ=
,解得λ=![]() .
.
所以当λ=![]() 时,二面角A﹣C1E﹣C的余弦值为
时,二面角A﹣C1E﹣C的余弦值为![]() .
.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目



