题目内容
【题目】[选修4—4:坐标系与参数方程]
在直角坐标系![]() 中,曲线
中,曲线![]() 的方程为
的方程为![]() .以坐标原点为极点,
.以坐标原点为极点,![]() 轴正半轴为极轴建立极坐标系,曲线
轴正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求![]() 的直角坐标方程;
的直角坐标方程;
(2)若![]() 与
与![]() 有且仅有三个公共点,求
有且仅有三个公共点,求![]() 的方程.
的方程.
【答案】 (1)![]() .
.
(2)综上,所求![]() 的方程为
的方程为![]() .
.
【解析】分析:(1)就根据![]() ,
,![]() 以及
以及![]() ,将方程
,将方程![]() 中的相关的量代换,求得直角坐标方程;
中的相关的量代换,求得直角坐标方程;
(2)结合方程的形式,可以断定曲线![]() 是圆心为
是圆心为![]() ,半径为
,半径为![]() 的圆,
的圆,![]() 是过点
是过点![]() 且关于
且关于![]() 轴对称的两条射线,通过分析图形的特征,得到什么情况下会出现三个公共点,结合直线与圆的位置关系,得到k所满足的关系式,从而求得结果.
轴对称的两条射线,通过分析图形的特征,得到什么情况下会出现三个公共点,结合直线与圆的位置关系,得到k所满足的关系式,从而求得结果.
详解:(1)由![]() ,
,![]() 得
得![]() 的直角坐标方程为
的直角坐标方程为
![]() .
.
(2)由(1)知![]() 是圆心为
是圆心为![]() ,半径为
,半径为![]() 的圆.
的圆.
由题设知,![]() 是过点
是过点![]() 且关于
且关于![]() 轴对称的两条射线.记
轴对称的两条射线.记![]() 轴右边的射线为
轴右边的射线为![]() ,
,![]() 轴左边的射线为
轴左边的射线为![]() .由于
.由于![]() 在圆
在圆![]() 的外面,故
的外面,故![]() 与
与![]() 有且仅有三个公共点等价于
有且仅有三个公共点等价于![]() 与
与![]() 只有一个公共点且
只有一个公共点且![]() 与
与![]() 有两个公共点,或
有两个公共点,或![]() 与
与![]() 只有一个公共点且
只有一个公共点且![]() 与
与![]() 有两个公共点.
有两个公共点.
当![]() 与
与![]() 只有一个公共点时,
只有一个公共点时,![]() 到
到![]() 所在直线的距离为
所在直线的距离为![]() ,所以
,所以![]() ,故
,故![]() 或
或![]() .
.
经检验,当![]() 时,
时,![]() 与
与![]() 没有公共点;当
没有公共点;当![]() 时,
时,![]() 与
与![]() 只有一个公共点,
只有一个公共点,![]() 与
与![]() 有两个公共点.
有两个公共点.
当![]() 与
与![]() 只有一个公共点时,
只有一个公共点时,![]() 到
到![]() 所在直线的距离为
所在直线的距离为![]() ,所以
,所以![]() ,故
,故![]() 或
或![]() .
.
经检验,当![]() 时,
时,![]() 与
与![]() 没有公共点;当
没有公共点;当![]() 时,
时,![]() 与
与![]() 没有公共点.
没有公共点.
综上,所求![]() 的方程为
的方程为![]() .
.

【题目】为了研究高中学生对乡村音乐的态度(喜欢和不喜欢两种态度)与性别的关系,运用2×2列联表进行独立性检验,经计算K2=8.01,附表如下:
P(K2≥k0) | 0.100 | 0.050 | 0.025 | 0.010 | 0.001 |
k0 | 2.706 | 3.841 | 5.024 | 6.635 | 10.828 |
参照附表,得到的正确的结论是( )
A. 有99%以上的把握认为“喜欢乡村音乐与性别有关”
B. 有99%以上的把握认为“喜欢乡村音乐与性别无关”
C. 在犯错误的概率不超过0.1%的前提下,认为“喜欢乡村音乐与性别有关”
D. 在犯错误的概率不超过0.1%的前提下,认为“喜欢乡村音乐与性别无关”
【题目】某大型水果超市每天以![]() 元/千克的价格从水果基地购进若干
元/千克的价格从水果基地购进若干![]() 水果,然后以
水果,然后以![]() 元/千克的价格出售,若有剩余,则将剩下的水果以
元/千克的价格出售,若有剩余,则将剩下的水果以![]() 元/千克的价格退回水果基地,为了确定进货数量,该超市记录了
元/千克的价格退回水果基地,为了确定进货数量,该超市记录了![]() 水果最近
水果最近![]() 天的日需求量(单位:千克),整理得下表:
天的日需求量(单位:千克),整理得下表:
日需求量 |
|
|
|
|
|
|
|
频数 |
|
|
|
|
|
|
|
以![]() 天记录的各日需求量的频率代替各日需求量的概率.
天记录的各日需求量的频率代替各日需求量的概率.
(1)求该超市![]() 水果日需求量
水果日需求量![]() (单位:千克)的分布列;
(单位:千克)的分布列;
(2)若该超市一天购进![]() 水果
水果![]() 千克,记超市当天
千克,记超市当天![]() 水果获得的利润为
水果获得的利润为![]() (单位:元),求
(单位:元),求![]() 的分布列及其数学期望.
的分布列及其数学期望.
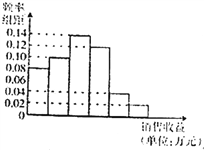
【题目】某公司为了解广告投入对销售收益的影响,在若干地区各投入![]() 万元广告费用,并将各地的销售收益(单位:万元)绘制成如图所示的频率分布直方图.由于工作人员操作失误,横轴的数据丢失,但可以确定横轴是从
万元广告费用,并将各地的销售收益(单位:万元)绘制成如图所示的频率分布直方图.由于工作人员操作失误,横轴的数据丢失,但可以确定横轴是从![]() 开始计数的.
开始计数的.
广告投入 | 1 | 2 | 3 | 4 | 5 |
销售收益 | 2 | 3 | 2 | 5 | 7 |
(Ⅰ)根据频率分布直方图计算图中各小长方形的宽度;
(Ⅱ)该公司按照类似的研究方法,测得另外一些数据,并整理得到上表:
表中的数据显示![]() 与
与![]() 之间存在线性相关关系,求
之间存在线性相关关系,求![]() 关于
关于![]() 的回归方程;
的回归方程;
(Ⅲ)若广告投入![]() 万元时,实际销售收益为
万元时,实际销售收益为![]() 万元,求残差
万元,求残差![]() .
.
附: ,
,![]()
【题目】某中学将100名髙一新生分成水平相同的甲、乙两个“平行班”,每班50人.陈老师采用A、B两种不同的教学方式分别在甲、乙两个班级进行教改实验.为了解教学效果,期末考试后,陈老师对甲、乙两个班级的学生成绩进行统计分析,画出频率分布直方图(如下图).记成绩不低于90分者为“成绩优秀”

| 0.05 | 0.01 | 0.001 |
| 3.841 | 6.635 | 10.828 |
(I)从乙班随机抽取2名学生的成绩,记“成绩优秀”的个数为![]() ,求
,求![]() 的分布列和数学期望;
的分布列和数学期望;
(II)根据频率分布直方图填写下面2 x2列联表,并判断是否有95%的把握认为:“成绩优秀”与教学方式有关.
甲班(A方式) | 乙班(B方式) | 总计 | |
成绩优秀 | |||
成绩不优秀 | |||
总计 |
附: 
