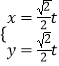题目内容
【题目】已知函数 ![]() ,x∈R,ω>0.
,x∈R,ω>0.
(1)求函数f(x)的值域;
(2)若函数y=f(x)的图象与直线y=﹣1的两个相邻交点间的距离为 ![]() ,求函数y=f(x)的单调区间.
,求函数y=f(x)的单调区间.
【答案】
(1)解:∵f(x)=函数 ![]() ,
,
=( ![]() )+(
)+( ![]() )﹣(cosωx+1),
)﹣(cosωx+1),
= ![]() …(4分),
…(4分),
∵x∈R,
∴ ![]() ,
,
∴ ![]() ,
,
∴函数y=f(x)的值域为[﹣3,1]
(2)解:∵由题设条件和三角函数图象和性质知:
函数y=f(x)的周期为π,
∴ ![]() ,
,
∴ ![]() ,
,
![]() ,
,
![]() ,
,
∴ ![]()
【解析】(1)根据凑角公式整理已知函数式转化为单一的三角函数,借助三角函数的值域得到结论。(2)由题设条件以及三角函数的图像和性质可得y=f(x)的周期为π,进而求出![]() 故得到f ( x )的解析式,再根据正弦函数的单调性由整体思想即可得出结果。
故得到f ( x )的解析式,再根据正弦函数的单调性由整体思想即可得出结果。
【考点精析】利用函数y=Asin(ωx+φ)的图象变换对题目进行判断即可得到答案,需要熟知图象上所有点向左(右)平移![]() 个单位长度,得到函数
个单位长度,得到函数![]() 的图象;再将函数
的图象;再将函数![]() 的图象上所有点的横坐标伸长(缩短)到原来的
的图象上所有点的横坐标伸长(缩短)到原来的![]() 倍(纵坐标不变),得到函数
倍(纵坐标不变),得到函数![]() 的图象;再将函数
的图象;再将函数![]() 的图象上所有点的纵坐标伸长(缩短)到原来的
的图象上所有点的纵坐标伸长(缩短)到原来的![]() 倍(横坐标不变),得到函数
倍(横坐标不变),得到函数![]() 的图象.
的图象.

练习册系列答案
 精英口算卡系列答案
精英口算卡系列答案 应用题点拨系列答案
应用题点拨系列答案 状元及第系列答案
状元及第系列答案
相关题目