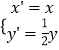题目内容
【题目】已知定义在R上的函数 
，若函数g（x）=f（x）﹣a（x+1）恰有2个零点，则实数a的取值范围是 ．
【答案】
∪{0}
【解析】解：数形结合，由直线y=a（x+1）与曲线y=f（x）的位置关系如图：x≤﹣1时，y=x2+x，y′=2x+1， 
=﹣1，
函数g（x）=f（x）﹣a（x+1）恰有2个零点，可得a≤﹣1；
当x∈（﹣1，0）时，y=﹣x2﹣x，y′=﹣2x﹣1， =2﹣1=1；
当x＞0时，y=ln（x+1），过（﹣1，0）点与曲线的切点为：（m，ln（m+1）），
y′= 
，
可得： 
= 
，可得m=e﹣1，
切线的斜率为： 
．函数g（x）=f（x）﹣a（x+1）恰有2个零点，可得a 
，
a=0时，函数的零点也是2个．
综上可得当 
∪{0}时有两个交点，即函数y=g（x）恰有两个零点．
所以答案是： 
∪{0}．
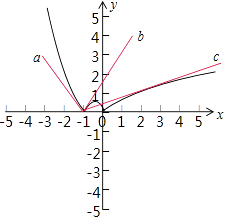
练习册系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案
相关题目
