题目内容
【题目】已知函数f(x)=|x﹣a|+ ![]() (a≠0).
(a≠0).
(1)若a=1,解关于x的不等式f(x)≥|x﹣2|;
(2)若不等式f(x)﹣f(x+m)≤1恒成立,求正数m的最大值.
【答案】
(1)解:函数f(x)=|x﹣a|+ ![]() (a≠0).
(a≠0).
当a=1时,可得f(x)=|x﹣1|+ ![]() ≥|x﹣2|,
≥|x﹣2|,
等价于 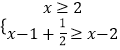 或
或 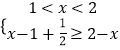 或
或 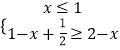
|解得:x ![]()
即原不等式的解集为[ ![]() ,+∞)
,+∞)
(2)解:不等式f(x)﹣f(x+m)≤1恒成立,即|x﹣a|+ ![]() ﹣|x+m﹣a|
﹣|x+m﹣a| ![]() =|x﹣a|﹣|x+m﹣a|≤|x﹣a﹣x﹣m+a|=m
=|x﹣a|﹣|x+m﹣a|≤|x﹣a﹣x﹣m+a|=m
∵f(x)﹣f(x+m)≤1恒成立,
则m≤1.
那么m的最大值为1
【解析】根据含有绝对值不等式的解法可得出不等式的解集。(2)由已知利用绝对值的性质整理可得m≤1即m的最大值为1。

练习册系列答案
相关题目