题目内容
【题目】已知函数![]() .
.
(1)若关于![]() 的不等式
的不等式![]() 恒成立,求
恒成立,求![]() 的取值范围;
的取值范围;
(2)当![]() 时,求证:
时,求证:![]() ;
;
(3)求证:![]() .
.
【答案】(1)![]() ;(2)见解析;(3)见解析.
;(2)见解析;(3)见解析.
【解析】
(1)不等式![]() 恒成立等价于
恒成立等价于![]() 恒成立,即
恒成立,即![]() ,再构造函数
,再构造函数![]() ,利用导数求其最小值即可得解;
,利用导数求其最小值即可得解;
(2)由(1)知当![]() 时,有
时,有![]() 恒成立,所以
恒成立,所以![]() ,然后令
,然后令![]() ,即
,即![]() ,再不等式左右两边分别累加求和即可得解;
,再不等式左右两边分别累加求和即可得解;
(3)由(1)可知,当![]() 时,
时, ![]() 在
在![]() 上恒成立,即要证
上恒成立,即要证![]() 等价于
等价于![]() ,即只需证当
,即只需证当![]() 时,
时,![]() ,再构造函数
,再构造函数![]() ,利用导数求证即可.
,利用导数求证即可.
解:(1)由题意,函数![]() 的定义域为
的定义域为![]() ,
,
由![]() ,得
,得![]() ,
,
所以![]() 恒成立,即
恒成立,即![]() .
.
令![]() ,则
,则![]() ,
,
令![]() ,解得
,解得![]() ,令
,令![]() ,解得
,解得![]() ,
,
所以函数![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 上单调递增.
上单调递增.
所以函数![]() 的最小值为
的最小值为![]() ,所以
,所以![]() ,
,
即![]() 的取值范围是
的取值范围是![]() .
.
(2)由(1)知当![]() 时,有
时,有![]() 恒成立,所以
恒成立,所以![]() (当且仅当
(当且仅当![]() 时等号成立).
时等号成立).
令![]() ,得
,得![]() ,
,
所以![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,
以上各式相加,得![]() ,
,
所以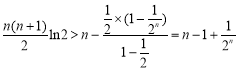 ,
,
即![]() .
.
(3)由(1)可知,当![]() 时,
时,![]() ,
,
即![]() 在
在![]() 上恒成立.
上恒成立.
要证![]() ,即证
,即证![]() ,
,
只需证当![]() 时,
时,![]() .
.
令![]() ,则
,则![]() .
.
令![]() ,则
,则![]() .
.
由![]() ,得
,得![]() .
.
当![]() 时,
时,![]() ,
,![]() 单调递减;
单调递减;
当![]() 时,
时,![]() ,
,![]() 单调递增.
单调递增.
即![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 上单调递增.
上单调递增.
而![]() ,
,![]() ,
,
所以![]() ,使得
,使得![]() .
.
当![]() 时,
时,![]() ,
,![]() 单调递增;
单调递增;
当![]() 时,
时,![]() ,
,![]() 单调递减;
单调递减;
当![]() 时,
时,![]() ,
,![]() 单调递增.
单调递增.
又![]() ,
,![]() ,
,
所以对![]() ,
,![]() 恒成立,即
恒成立,即![]() .
.
综上所述,![]() 成立.
成立.

【题目】某社区消费者协会为了解本社区居民网购消费情况,随机抽取了100位居民作为样本,就最近一年来网购消费金额(单位:千元),网购次数和支付方式等进行了问卷调査.经统计这100位居民的网购消费金额均在区间![]() 内,按
内,按![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 分成6组,其频率分布直方图如图所示.
分成6组,其频率分布直方图如图所示.
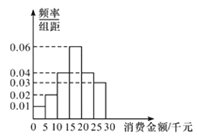
(1)估计该社区居民最近一年来网购消费金额的中位数;
(2)将网购消费金额在20千元以上者称为“网购迷”,补全下面的![]() 列联表,并判断有多大把握认为“网购迷与性别有关系”;
列联表,并判断有多大把握认为“网购迷与性别有关系”;
男 | 女 | 合计 | |
网购迷 | 20 | ||
非网购迷 | 45 | ||
合计 | 100 |
(3)调査显示,甲、乙两人每次网购采用的支付方式相互独立,两人网购时间与次数也互不. 影响.统计最近一年来两人网购的总次数与支付方式,所得数据如下表所示:
网购总次数 | 支付宝支付次数 | 银行卡支付次数 | 微信支付次数 | |
80 | 40 | 16 | 24 | |
乙 | 90 | 60 | 18 | 12 |
将频率视为概率,若甲、乙两人在下周内各自网购2次,记两人采用支付宝支付的次数之和为![]() ,求
,求![]() 的数学期望.
的数学期望.
附:观测值公式: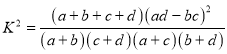
临界值表:
| 0.01 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |