题目内容
【题目】在平面直角坐标系中,若![]() ,
,![]() ,且
,且![]() .
.
(Ⅰ)求动点![]() 的轨迹
的轨迹![]() 的方程;
的方程;
(Ⅱ)设(Ⅰ)中曲线![]() 的左、右顶点分别为
的左、右顶点分别为![]() 、
、![]() ,过点
,过点![]() 的直线
的直线![]() 与曲线
与曲线![]() 交于两点
交于两点![]() ,
,![]() (不与
(不与![]() ,
,![]() 重合).若直线
重合).若直线![]() 与直线
与直线![]() 相交于点
相交于点![]() ,试判断点
,试判断点![]() ,
,![]() ,
,![]() 是否共线,并说明理由.
是否共线,并说明理由.
【答案】(Ⅰ)![]() (Ⅱ)见解析
(Ⅱ)见解析
【解析】
第(Ⅰ)问由且![]() 可得点到两定点的距离之和为常数,可得动点轨迹为椭圆;
可得点到两定点的距离之和为常数,可得动点轨迹为椭圆;
第(Ⅱ)问分类讨论直线![]() 的方程,斜率不存在时可直接求出所需点的坐标;斜率存在时则先设出直线方程,联立直线方程与椭圆方程求出交点关系,再求出点
的方程,斜率不存在时可直接求出所需点的坐标;斜率存在时则先设出直线方程,联立直线方程与椭圆方程求出交点关系,再求出点![]() ,利用
,利用![]() 的关系判断即可.
的关系判断即可.
解:(Ⅰ)设![]() ,
,![]() ,则
,则
![]()
![]() .
.
∴动点![]() 的轨迹是以
的轨迹是以![]() ,
,![]() 为焦点的椭圆,
为焦点的椭圆,
设其方程为![]() ,则
,则![]() ,
,![]() ,即
,即![]() ,
,![]() ,
,
∴![]() .∴动点
.∴动点![]() 的轨迹
的轨迹![]() 的方程为
的方程为![]() .
.
(Ⅱ)①当直线![]() 的斜率不存在时,
的斜率不存在时,![]() :
:![]() ,不妨设
,不妨设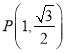 ,
, ,
,
∴直线![]() 的方程为
的方程为![]() ,
,
令![]() 得
得![]() .
.
∴![]() .∴点
.∴点![]() ,
,![]() ,
,![]() 共线.
共线.
②当直线![]() 的斜率存在时,设
的斜率存在时,设![]() :
:![]() ,设
,设![]() ,
,![]() .
.
由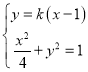 消
消![]() 得
得![]() ,
,
由题意知![]() 恒成立,故
恒成立,故![]() ,
,![]() ,
,
∴直线![]() 的方程为
的方程为![]() ,
,
令![]() 得
得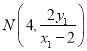 .
.
∴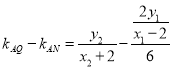
![]() ,
,
上式中的分子![]()
![]()
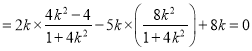 .
.
∴![]() ,∴点
,∴点![]() ,
,![]() ,
,![]() 共线.
共线.
综上可知,点![]() ,
,![]() ,
,![]() 共线.
共线.

练习册系列答案
 同步轻松练习系列答案
同步轻松练习系列答案 课课通课程标准思维方法与能力训练系列答案
课课通课程标准思维方法与能力训练系列答案
相关题目
【题目】为调查某地区老人是否需要志愿者提供帮助,用简单随机抽样方法从该地区调查了500位老年人,结果如下:
是否需要志愿 性别 | 男 | 女 |
需要 | 40 | 30 |
不需要 | 160 | 270 |
(1)估计该地区老年人中,需要志愿者提供帮助的老年人的比例;
(2)能否有99%的把握认为该地区的老年人是否需要志愿者提供帮助与性别有关?
(3)根据(2)的结论,能否提供更好的调查方法来估计该地区老年人中,需要志愿帮助的老年人的比例?说明理由.
P | 0.0 | 0.010 | 0.001 |
k | 3.841 | 6.635 | 10.828 |