题目内容

11．直线l经过抛物线y=x2-3x+1与y轴的交点，且与直线x+2y=0平行，则直线l的方程是x+2y-2=0．

分析 通过直线l与直线x+2y=0平行，可设直线l方程，代入抛物线y=x2-3x+1与y轴的交点为（0，1），计算即可．

解答 解：∵抛物线y=x2-3x+1与y轴的交点为（0，1），
∴直线l经过（0，1），
又∵直线l与直线x+2y=0平行，
∴可设直线l方程为：x+2y+a=0，
代入点（0，1），即：0+2+a=0，
∴a=-2，即直线l方程为：x+2y-2=0，
故答案为：x+2y-2=0．

点评 本题考查求直线的方程，注意解题方法的积累，属于基础题．

练习册系列答案
相关题目
1．命题p：$\overrightarrow{AB}$•$\overrightarrow{AC}$＜0，命题q：∠BAC是钝角．p是q的（　　）
A．充分不必要条件B．必要不充分条件
C．充要条件D．既不充分也不必要条件
2．若点（-2，-1）是圆（x+1）2+y2=1的弦AB的中点，则直线AB的方程为（　　）
A．x-y+1=0B．3x+y+7=0C．x+y+3=0D．x-3y-1=0
19．设两个非零向量$\overrightarrow a$与$\overrightarrow b$不共线，若$\overrightarrow{AB}=\overrightarrow a+\overrightarrow b，\overrightarrow{BC}=2\overrightarrow a+8\overrightarrow b，\overrightarrow{CD}$=$3（\overrightarrow a-\overrightarrow b）$，则（　　）
A．A，B，C三点共线B．B，C，D三点共线C．A，C，D三点共线D．A，B，D三点共线
6．设平面向量组ai （i=1，2，3，…）满足：①|ai|=1；②ai•ai+1=0，设Tn=|a1+a2+…+an|（n≥2），则T4的最大值为$2\sqrt{2}$．
16．已知函数f（x）=$\sqrt{3}$sin（ωx+φ）+2sin2$\frac{ωx+φ}{2}$-1（ω＞0，0＜φ＜π），相邻两对称轴间的距离为$\frac{π}{2}$，且f（0）=0
（1）求f（x）的解析式；
（2）将函数y=f（x）的图象沿x轴方向向右平移$\frac{π}{6}$个单位长度，再把横坐标缩短到原来的$\frac{1}{2}$（纵坐标不变），得到函数y=g（x）的图象．当x∈[-$\frac{π}{12}，\frac{π}{6}$]时，求函数g（x）的值域．
3．用不等号（＞，＜）填空：$\frac{sin100°}{sin200°cos300°cos100°}$＞0．
20．求证：1+$\frac{1}{3^2}$+$\frac{1}{5^2}$+…+$\frac{1}{（2n-1）^2}$＞$\frac{7}{6}$-$\frac{1}{2（2n+1）}$．
1．阅读如图所示的程序框图，若输入m=6，则输出S等于（　　）
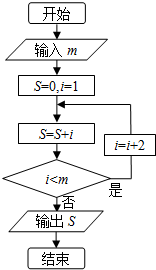
A．4B．9C．16D．25

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网