题目内容
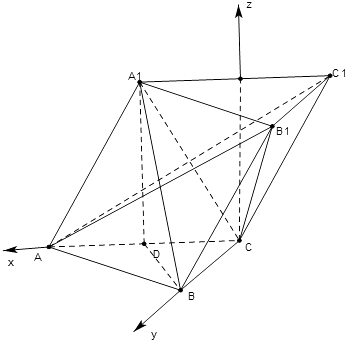
【题目】如图,三棱柱中ABC﹣A1B1C1中,点A1在平面ABC内的射影D为棱AC的中点,侧面A1ACC1为边长为2的菱形,AC⊥CB,BC=1. 
(1)证明:AC1⊥平面A1BC;
(2)求二面角B﹣A1C﹣B1的大小.
【答案】
(1)解:由题意得A1D⊥平面ABC,
∴平面A1ACC1⊥平面ABC,
∵平面A1ACC1∩平面ABC=AC,CA⊥CB
∴BC⊥平面A1ACC1
∴BC⊥AC1
连接A1C
∵侧面A1ACC1为菱形
∴A1C⊥AC1,
∴AC1⊥平面A1BC,
(2)解:直角三角形A1AD中,
∵AA1=2,AD=1,∴A1D= ![]() ,
,
过C作CM∥A1D交A1C1于M点,
分别以C为坐标原点,以CA,CB,CM的方向为x轴,y轴,z轴正方向建立如图所示的空间直角坐标系C﹣xyz,
则C(0,0,0),B(0,1,0),D(1,0,0),A(2,0,0),A1(1,0, ![]() ),
),
由 ![]() =
= ![]() ,得C1(﹣1,0,
,得C1(﹣1,0, ![]() ),∴
),∴ ![]() =(﹣3,0,
=(﹣3,0, ![]() ),
),
由 ![]() =
= ![]() 得B1(﹣1,1,
得B1(﹣1,1, ![]() ),∴
),∴ ![]() =(﹣1,1,
=(﹣1,1, ![]() ),
), ![]() =(1,0,
=(1,0, ![]() ),设平面A1B1C的一个法向量为
),设平面A1B1C的一个法向量为 ![]() =(x,y,z),
=(x,y,z),
由 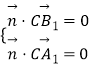 得
得 ![]() ,
,
令z=1,解得 ![]() =(﹣
=(﹣ ![]() ,﹣2
,﹣2 ![]() ,1)
,1)
由题得 ![]() =
= ![]() =(﹣3,0,
=(﹣3,0, ![]() )为平面A1BC的一个法向量, cos<
)为平面A1BC的一个法向量, cos< ![]() ,
, ![]() >=
>= ![]() =
= ![]() =
= ![]() =
= ![]() ,
,
则< ![]() ,
, ![]() >=
>= ![]() .
.
因此二面角B﹣A1C﹣B1的大小为 ![]() .
.
【解析】(1)根据线面垂直的判定定理即可得到结论.(2)建立坐标系,求出平面的法向量,利用向量法进行求解即可.
【考点精析】认真审题,首先需要了解直线与平面垂直的判定(一条直线与一个平面内的两条相交直线都垂直,则该直线与此平面垂直;注意点:a)定理中的“两条相交直线”这一条件不可忽视;b)定理体现了“直线与平面垂直”与“直线与直线垂直”互相转化的数学思想).

【题目】菜农定期使用低害杀虫农药对蔬菜进行喷洒,以防止害虫的危害,但蔬菜上市时蔬菜仍存有少量的残留农药,食用时需要用清水清洗干净,下表是用清水![]() (单位:千克)清洗蔬菜1千克后,蔬菜上残留的农药
(单位:千克)清洗蔬菜1千克后,蔬菜上残留的农药![]() (单位:微克)的统计表:
(单位:微克)的统计表:
| 1 | 2 | 3 | 4 | 5 |
| 58 | 54 | 39 | 29 | 10 |

(1)在答题纸的坐标系中,描出散点图,并判断变量![]() 与
与![]() 是正相关还是负相关;
是正相关还是负相关;
(2)若用解析式![]() 作为蔬菜农药残量
作为蔬菜农药残量![]() 与用水量
与用水量![]() 的回归方程,令
的回归方程,令![]() ,计算平均值
,计算平均值![]() 与
与![]() ,完成以下表格(填在答题卡中),求出
,完成以下表格(填在答题卡中),求出![]() 与
与![]() 的回归方程.(
的回归方程.(![]() ,
, ![]() 保留两位有效数字):
保留两位有效数字):
| 1 | 4 | 9 | 16 | 25 |
| 58 | 54 | 39 | 29 | 10 |
| |||||
|
(3)对于某种残留在蔬菜上的农药,当它的残留量低于20微克时对人体无害,为了放心食用该蔬菜,请评估需要用多少千克的清水清洗一千克蔬菜?(精确到0.1,参考数据![]() )(附:对于一组数据
)(附:对于一组数据![]() ,
, ![]() ,……,
,……, ![]() ,其回归直线
,其回归直线![]() 的斜率和截距的最小二乘法估计分别为:
的斜率和截距的最小二乘法估计分别为:  ,
, ![]() )
)

