题目内容
【题目】定义在![]() 上的函数
上的函数![]() ,如果满足:对任意
,如果满足:对任意![]() ,存在常数
,存在常数![]() ,都有
,都有![]() 成立,则称
成立,则称![]() 是
是![]() 上的有界函数,其中
上的有界函数,其中![]() 称为函数
称为函数![]() 的一个上界.已知函数
的一个上界.已知函数![]() ,
, ![]() .
.
(1)若函数![]() 为奇函数,求实数
为奇函数,求实数![]() 的值;
的值;
(2)在(1)的条件下,求函数![]() 在区间
在区间![]() 上的所有上界构成的集合;
上的所有上界构成的集合;
(3)若函数![]() 在
在![]() 上是以3为上界的有界函数,求实数
上是以3为上界的有界函数,求实数![]() 的取值范围.
的取值范围.
【答案】(1)![]() ;(2)上界构成集合为
;(2)上界构成集合为![]() ;(3)实数
;(3)实数![]() 的取值范围为
的取值范围为![]() .
.
【解析】试题分析:(1)![]() ,即
,即![]() ,得
,得![]() ;(2)函数
;(2)函数![]() 在区间
在区间![]() 上单调递增,所以值域为
上单调递增,所以值域为![]() ,所以所有上界构成集合为
,所以所有上界构成集合为![]() ;(3)
;(3)![]() 在
在![]() 上恒成立,分离参数得
上恒成立,分离参数得![]() 在
在![]() 上恒成立,所以
上恒成立,所以![]() 的取值范围为
的取值范围为![]() .
.
试题解析:
(1)因为函数![]() 为奇函数,
为奇函数,
所以![]() ,即
,即![]() ,
,
即![]() ,得
,得![]() ,而当
,而当![]() 时不合题意,故
时不合题意,故![]() .
.
(2)由(1)得: ![]() ,
,
易知,函数![]() 在区间
在区间![]() 上单调递增,
上单调递增,
所以函数![]() 在区间
在区间![]() 上单调递增,
上单调递增,
所以函数![]() 在区间
在区间![]() 上的值域为
上的值域为![]() ,
,
所以![]() ,故函数
,故函数![]() 在区间
在区间![]() 上的所有上界构成集合为
上的所有上界构成集合为![]() .
.
(3)由题意知, ![]() 在
在![]() 上恒成立.
上恒成立.
![]() ,
, ![]() .
.
∴![]() 在
在![]() 上恒成立.
上恒成立.
∴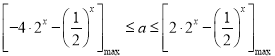
设![]() ,
, ![]() ,
, ![]() ,由
,由![]() 得
得![]() ,
,
设![]() ,
, ![]() ,
,
![]() ,
,
所以![]() 在
在![]() 上递减,
上递减, ![]() 在
在![]() 上递增,
上递增,
![]() 在
在![]() 上的最大值为
上的最大值为![]() ,
, ![]() 在
在![]() 上的最小值为
上的最小值为![]() .
.
所以实数![]() 的取值范围为
的取值范围为![]() .
.

练习册系列答案
相关题目
【题目】某食品企业一个月内被消费者投诉的次数用![]() 表示.据统计,随机变量
表示.据统计,随机变量![]() 的概率分布如下表所示.
的概率分布如下表所示.
| 0 | 1 | 2 | 3 |
| 0.1 | 0.3 |
|
|
(1)求![]() 的值和
的值和![]() 的数学期望;
的数学期望;
(2)假设一月份与二月份被消费者投诉的次数互不影响,求该企业在这两个月内共被消费者投诉2次的概率.