题目内容
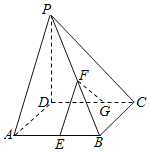
【题目】如图1，在矩形ABCD中，AB＝4，AD＝2，E是CD的中点，将△ADE沿AE折起，得到如图2所示的四棱锥D1—ABCE，其中平面D1AE⊥平面ABCE.
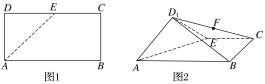
(1)证明：BE⊥平面D1AE；
(2)设F为CD1的中点，在线段AB上是否存在一点M，使得MF∥平面D1AE，若存在，求出
的值；若不存在，请说明理由．
【答案】（1）证明见解析（2）线段AB上存在满足题意的点M，且
＝
【解析】
（1）先计算得BE⊥AE，再根据面面垂直性质定理得结果，（2）先分析确定点M位置，再取D1E的中点L，根据平几知识得AMFL为平行四边形，最后根据线面平行判定定理得结果.
(1)证明连接BE，
∵ABCD为矩形且AD＝DE＝EC＝BC＝2，
∴∠AEB＝90°，即BE⊥AE，
又平面D1AE⊥平面ABCE，
平面D1AE∩平面ABCE＝AE，BE平面ABCE，
∴BE⊥平面D1AE.
(2)解AM＝AB，取D1E的中点L，连接AL，FL，
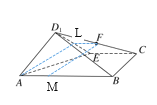
∵FL∥EC，EC∥AB，∴FL∥AB且FL＝AB，
∴FL∥AM，FL=AM
∴AMFL为平行四边形，∴MF∥AL，
因为MF不在平面AD1E上， AL平面AD1E，所以MF∥平面AD1E.
故线段AB上存在满足题意的点M，且＝.
练习册系列答案
相关题目
