题目内容
【题目】已知点P为椭圆C:![]() 1(a>b>0)上一点,F1,F2分别是椭圆C的左、右两个焦点,|PF1|=2|PF2|,且cos∠F1PF2
1(a>b>0)上一点,F1,F2分别是椭圆C的左、右两个焦点,|PF1|=2|PF2|,且cos∠F1PF2![]() ,过点F2且斜率为k的直线l与椭圆C交于A,B两点.
,过点F2且斜率为k的直线l与椭圆C交于A,B两点.
(1)求椭圆C的离心率;
(2)若点M(1,![]() )在C上,求△MAB面积的最大值.
)在C上,求△MAB面积的最大值.
【答案】(1)![]() .(2)3
.(2)3
【解析】
(1)由余弦定理得![]() ,
,![]() 与
与![]() 关系,求出
关系,求出![]() ,
,![]() 的比值即是离心率的值;(2)由题意设直线与椭圆联立求出弦长,再求
的比值即是离心率的值;(2)由题意设直线与椭圆联立求出弦长,再求![]() 到直线
到直线![]() 距离求出面积,再利用函数的单调性求出面积的最大值.
距离求出面积,再利用函数的单调性求出面积的最大值.
(1)在△PF1F2中,设|PF2|=x,则|PF1|=2x,cos∠F1PF2![]() ,
,
由余弦定理得,(2c)2=x2+(2x)2﹣2x2xcos∠F1PF2=5x2﹣4x2![]() ,
,
∴x![]() c,2x
c,2x![]() c,所以2a=x+2x=4c∴e
c,所以2a=x+2x=4c∴e![]() ,
,
所以椭圆的离心率为![]() .
.
(2)由(1)得:b2=a2﹣c2=3c2,椭圆的方程为:![]() 1,
1,
点M在椭圆上,![]() 1,
1,
∴c2=1,b2=3,a2=4,
所以椭圆的方程为![]() 1.右焦点(1,0),
1.右焦点(1,0),
设直线l的方程:y=k(x﹣1),A(x,y),B(x',y'),
当k=0时,|AB|=2a=4,M到l的距离为![]() ,S△MAB
,S△MAB![]() 3,
3,
当k≠0时,联立与椭圆的方程整理得(3+4k2)x2﹣8k2x+4k2﹣12=0,
所以x+x'![]() ,xx'
,xx'![]() ,
,
弦长|AB|![]() |x﹣x'|
|x﹣x'|![]() 12
12![]() ,
,
M在直线l的距离d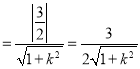 ,
,
所以S△MAB![]() |AB|d=9
|AB|d=9![]() 9
9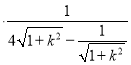 ,
,
设t=![]()
![]() ,
,
 ,分母是一个增函数(增函数+增函数=增函数),
,分母是一个增函数(增函数+增函数=增函数),
所以![]() 是一个减函数,
是一个减函数,
所以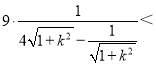 9
9![]() 3,
3,
综上△MAB面积的最大值为3.

【题目】某高校随机抽取部分男生测试立定跳远,将成绩整理得到频率分布表如表,测试成绩在220厘米以上(含220厘米)的男生定为“合格生”,成绩在260厘米以上(含260厘米)的男生定为“优良生”.
分组(厘米) | 频数 | 频率 |
[180,200) | 0.10 | |
[200,220) | 15 | |
[220,240) | 0.30 | |
[240,260) | 0.30 | |
[260,280) | 0.20 | |
合计 | 1.00 |
(1)求参加测试的男生中“合格生”的人数.
(2)从参加测试的“合格生”中,根据表中分组情况,按分层抽样的方法抽取8名男生,再从这8名男生中抽取3名男生,记X表示3人中“优良生”的人数,求X的分布列及数学期望.