题目内容
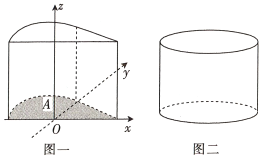
【题目】我国古代数学家祖暅提出原理：“幂势既同，则积不容异”.其中“幂”是截面积，“势”是几何体的高.该原理的意思是：夹在两个平行平面间的两个几何体，被任一平行于这两个平行平面的平面所截，若所截的两个截面的面积恒相等，则这两个几何体的体积相等.如图，在空间直角坐标系中的
平面内，若函数
的图象与
轴围成一个封闭的区域
，将区域沿
轴的正方向平移8个单位长度，得到几何体如图一，现有一个与之等高的圆柱如图二，其底面积与区域的面积相等，则此圆柱的体积为__________．
【答案】
【解析】
利用四分之一圆的面积和直角三角形面积公式求得阴影部分的面积，进而求得圆柱的体积.
表示的是四分之一的圆的面积，且圆的半径是
，所以区域
的面积为
，所以圆柱的体积
.
练习册系列答案
智趣暑假温故知新系列答案
英语小英雄天天默写系列答案
暑假作业安徽少年儿童出版社系列答案
相关题目
【题目】某电子商务平台的管理员随机抽取了1000位上网购物者，并对其年龄（在10岁到69岁之间）进行了调查，统计情况如下表所示.
年龄 |
|
|
|
|
|
|
人数 | 100 | 150 |
| 200 |
| 50 |
已知
，
，
三个年龄段的上网购物的人数依次构成递减的等比数列.
（1）求
的值；
（2）若将年龄在
内的上网购物者定义为“消费主力军”，其他年龄段内的上网购物者定义为“消费潜力军”.现采用分层抽样的方式从参与调查的1000位上网购物者中抽取5人，再从这5人中抽取2人，求这2人中至少有一人是消费潜力军的概率.
