题目内容
【题目】设![]() ,若
,若![]() 时,恒有
时,恒有![]() ,则
,则![]() .
.
【答案】-1
【解析】
试题分析:验证发现,
当x=1时,将1代入不等式有0≤a+b≤0,所以a+b=0,
当x=0时,可得0≤b≤1,结合a+b=0可得-1≤a≤0,
令f(x)=x4-x3+ax+b,即f(1)=a+b=0,
又f′(x)=4x3-3x2+a,f′′(x)=12x2-6x,
令f′′(x)>0,可得x>![]() ,则f′(x)=4x3-3x2+a在[0,
,则f′(x)=4x3-3x2+a在[0,![]() ]上减,在[
]上减,在[![]() ,+∞)上增,
,+∞)上增,
又-1≤a≤0,所以f′(0)=a<0,f′(1)=1+a≥0,
又x≥0时恒有![]() ,结合f(1)=a+b=0知,1必为函数f(x)=x4-x3+ax+b的极小值点,也是最小值点.
,结合f(1)=a+b=0知,1必为函数f(x)=x4-x3+ax+b的极小值点,也是最小值点.
故有f′(1)=1+a=0,由此得a=-1,b=1,
故ab=-1.

练习册系列答案
相关题目
【题目】已知函数![]() 的定义域
的定义域![]() ,部分对应值如表,
,部分对应值如表, ![]() 的导函数
的导函数![]() 的图象如图所示,下列关于函数
的图象如图所示,下列关于函数![]() 的命题;
的命题;
|
|
|
|
|
|
|
|
|
|
|
|
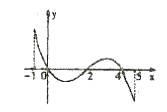
①函数![]() 的值域为
的值域为![]() ;
;
②函数![]() 在
在![]() 上是减函数;
上是减函数;
③如果当![]() 时,
时, ![]() 最大值是
最大值是![]() ,那么
,那么![]() 的最大值为
的最大值为![]() ;
;
④当![]() 时,函数
时,函数![]() 最多有4个零点.
最多有4个零点.
其中正确命题的序号是_________.