Question

【题目】已知椭圆的离心率为，椭圆C的长轴长为4．

（1）求椭圆的方程；

（2）已知直线与椭圆交于A，B两点，是否存在实数k使得以线段AB 为直径的圆恰好经过坐标原点O？若存在，求出k的值；若不存在，请说明理由

Answer 1

【答案】（1）（2）当时，以线段AB为直径的圆恰好经过坐标原点O

【解析】

试题分析：（1）设椭圆的焦半距为c，利用离心率为，椭圆C的长轴长为4．列出方程组求解c，推出b，即可得到椭圆的方程；（2）存在实数k使得以线段AB为直径的圆恰好经过坐标原点O．设点A，B，将直线l的方程代入，化简，利用韦达定理，结合向量的数量积为0，转化为．求解即可

试题解析：（1）设椭圆的焦半距为c，则由题设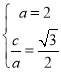，得，解得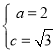，………2分

所以，故所求椭圆C的方程为．…………..4分

（2）存在实数k使得以线段AB为直径的圆恰好经过坐标原点O．理由如下：

设点，，将直线的方程代入，

并整理，得．（*）………………………………….6分

则，．………………………………………8分

因为以线段AB为直径的圆恰好经过坐标原点O，所以，即．

又,于是，…………….10分

解得，………………………………..11分

经检验知：此时（*）式的Δ＞0，符合题意．

所以当时，以线段AB为直径的圆恰好经过坐标原点O．………………12分