Question

【题目】对于任意实数x，符号[x]表示不超过x的最大整数，如[2.2]=2，[﹣3.5]=﹣4，设数列{an}的通项公式为an=[log21]+[log22]+[log23]+…[log2（2n﹣1）]．
（1）求a1a2a3的值；
（2）是否存在实数a，使得an=（n﹣2）2n+a（n∈N*），并说明理由．

Answer 1

【答案】
（1）解： a1=[log21]=0，a2=[log21]+[log22]+[log23]=0+1+1=2，

a3=[log21]+[log22]+[log23]+…+[log27]=0+1+1+2+2+2+2=10．

∴a1a2a3=0．

（2）解：当2n﹣1≤x≤2n﹣1时，[log2x]=n﹣1．

∴[log22n﹣1]+[log22n﹣1+1]+[log22n﹣1+2]+…+[log2（2n﹣1）]=（n﹣1）（2n﹣1﹣2n﹣1+1）=2n﹣1（n﹣1）．

∴an=10+21+222+233+…+2n﹣1（n﹣1），①

∴2an=221+232+243+…+2n（n﹣1），②

②﹣①得：an=﹣22﹣23﹣24﹣…﹣2n﹣1+2n（n﹣1）﹣2

=﹣ +2n（n﹣1）﹣2

=2n（n﹣2）+2．

又an=（n﹣2）2n+a，

∴a=2．

【解析】（1）计算a1=0，故a1a2a3=0；（2）根据对数性质得出an=10+21+222+233+…+2n﹣1（n﹣1），使用错位相减法求出an ， 得出a的值．
【考点精析】掌握数列的前n项和和数列的通项公式是解答本题的根本，需要知道数列{an}的前n项和sn与通项an的关系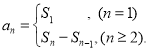；如果数列an的第n项与n之间的关系可以用一个公式表示，那么这个公式就叫这个数列的通项公式．