Question

【题目】在平面直角坐标系中，已知椭圆（）与直线： （），四点， ， ， 中有三个点在椭圆上，剩余一个点在直线上.

（Ⅰ）求椭圆的方程；

（Ⅱ）若动点在直线上，过作直线交椭圆于， 两点，使得，再过作直线，证明：直线恒过定点，并求出该定点的坐标.

Answer 1

【答案】（Ⅰ）;（Ⅱ）见解析.

【解析】试题分析：(1)判断点， ,点在椭圆C上,点在直线上,代入椭圆方程,即可求出椭圆的方程;
(2)分类讨论,利用点差法求出直线的方程,可得直线恒过定点.

试题解析：（Ⅰ）解：由题意有3个点在椭圆C上，

根据椭圆的对称性，则点， 一定在椭圆C上，

即，①

若点在椭圆C上，

则点必为椭圆C的左顶点，

而，则点一定不在椭圆C上，

故点在椭圆C上，点在直线l上，

所以，②

联立①②可解得， ，

所以椭圆C的方程为．

（Ⅱ）证明：由（Ⅰ）可得直线l的方程为，

设， ，

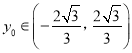当时，设， ，显然，

联立

则，即，

又，即P为线段MN的中点，

故直线MN的斜率为，

又，所以直线的方程为，

即，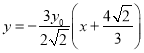

显然恒过定点；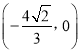

当时，直线MN即，此时为x轴亦过点，

综上所述， 恒过定点．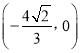

点睛:定点、定值问题通常是通过设参数或取特殊值来确定“定点”是什么、“定值”是多少，或者将该问题涉及的几何式转化为代数式或三角问题，证明该式是恒定的. 定点、定值问题同证明问题类似，在求定点、定值之前已知该值的结果，因此求解时应设参数，运用推理，到最后必定参数统消，定点、定值显现.