题目内容
16.在△ABC中,$AC=\sqrt{7}$,B=60°,BC边上的高$h=\frac{{3\sqrt{3}}}{2}$,则BC=1或2.分析 先求出AB,再在△ABC中,由余弦定理可得BC2-3BC+2=0,即可得出结论.
解答  解:∵B=60°,BC边上的高$h=\frac{{3\sqrt{3}}}{2}$,
解:∵B=60°,BC边上的高$h=\frac{{3\sqrt{3}}}{2}$,
∴AB=3
在△ABC中,由余弦定理可得,
AC2=AB2+BC2-2AB•BCcosB,
把已知AC=$\sqrt{7}$,AB=3,B=60°代入可得,
7=32+BC2-2×3×BC×$\frac{1}{2}$,
整理可得,BC2-3BC+2=0,
∴BC=1或2.
故答案为1或2.
点评 本题主要考查了余弦定理在解三角形中的应用,解答本题的关键是求出AB,属于基础试题.

练习册系列答案
 浙江名校名师金卷系列答案
浙江名校名师金卷系列答案
相关题目
7.若a∈R,则“a2>a”是“a>1”的( )条件.
| A. | 充分不必要 | B. | 必要不充分 | ||
| C. | 充要 | D. | 既不充分也不必要 |
5.某种产品的广告费用支出X与销售额之间有如下的对应数据:
(1)画出散点图;
(2)求回归直线方程;
(3)据此估计广告费用为10销售收入y的值.
参考公式:最小二乘法得$\left\{\begin{array}{l}{\widehat{b}=\frac{\sum_{i=1}^{n}({x}_{i}-\overline{x})({y}_{i}-\overline{y})}{\sum_{i=1}^{n}({x}_{i}-\overline{x})^{2}}=\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{x}\overline{y}}{\sum_{i=1}^{n}{{x}_{i}}^{2}-n\overline{{x}^{2}}}}\\{\widehat{a}=\overline{y}-\widehat{b}\overline{x}}\end{array}\right.$其中:$\widehat{b}$是回归方程的斜率,$\widehat{a}$是截距.
| x | 2 | 4 | 5 | 6 | 8 |
| y | 30 | 40 | 60 | 50 | 70 |
(2)求回归直线方程;
(3)据此估计广告费用为10销售收入y的值.
参考公式:最小二乘法得$\left\{\begin{array}{l}{\widehat{b}=\frac{\sum_{i=1}^{n}({x}_{i}-\overline{x})({y}_{i}-\overline{y})}{\sum_{i=1}^{n}({x}_{i}-\overline{x})^{2}}=\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{x}\overline{y}}{\sum_{i=1}^{n}{{x}_{i}}^{2}-n\overline{{x}^{2}}}}\\{\widehat{a}=\overline{y}-\widehat{b}\overline{x}}\end{array}\right.$其中:$\widehat{b}$是回归方程的斜率,$\widehat{a}$是截距.
6.正方体中相邻两个面上的对角线所成的角的大小为( )
| A. | 60° | B. | 45° | C. | 90° | D. | 30° |
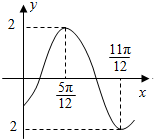 函数f(x)=2sin(ωx+φ)(ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示,则f(0)的值是-$\sqrt{3}$.
函数f(x)=2sin(ωx+φ)(ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示,则f(0)的值是-$\sqrt{3}$.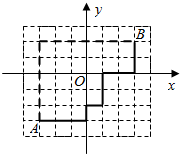 现代城市大多是棋盘式布局(如上海道路几乎都是东西和南北走向).在这样的城市中,我们说的两点间的距离往往不是指两点间的直线距离(位移),而是实际路程(如图).在直角坐标平面内,我们定义A(x1,y1)、B(x2,y2)两点间的“直角距离”为:D(AB)=|x1-x2|+|y1-y2|.
现代城市大多是棋盘式布局(如上海道路几乎都是东西和南北走向).在这样的城市中,我们说的两点间的距离往往不是指两点间的直线距离(位移),而是实际路程(如图).在直角坐标平面内,我们定义A(x1,y1)、B(x2,y2)两点间的“直角距离”为:D(AB)=|x1-x2|+|y1-y2|.