题目内容
过抛物线y2=2px(p>0)的焦点作倾斜角为30°的直线l与抛物线交于P,Q两点,分别作PP¢、QQ¢垂直于抛物线的准线于P¢、Q¢,若|PQ|=2,则四边形PP¢Q¢Q的面积为
| A.1 | B.2 | C. | D.3 |
A
解析试题分析:如图F( ,0),直线PQ方程为y=
,0),直线PQ方程为y=  (x-
(x- ),代入y2=2px整理得
),代入y2=2px整理得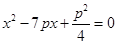 ,
,
设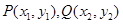 ,则
,则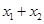 ="7p,"
="7p,"  ,
,
所以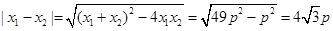 ,
,
由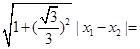 2,得
2,得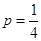 。所以梯形的高为
。所以梯形的高为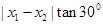 =
= ×
× =1,故四边形PP¢Q¢Q的面积为
=1,故四边形PP¢Q¢Q的面积为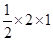 =1,故选A。
=1,故选A。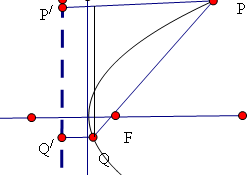
考点:本题主要考查抛物线的定义,直线与抛物线的位置关系,弦长公式。
点评:中档题,所得四边形是梯形,且上下底边和为PQ=2,因此,只需求梯形的高。通过联立方程组,应用韦达定理、弦长公式,达到解题目的。

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
抛物线 的焦点为
的焦点为 ,其上的动点
,其上的动点 在准线上的射影为
在准线上的射影为 ,若
,若 是等边三角形,则
是等边三角形,则 的横坐标是( )
的横坐标是( )
A. | B. | C. | D. |
若直线mx- ny = 4与⊙O: x2+y2= 4没有交点,则过点P(m,n)的直线与椭圆 的交点个数是 ( )
的交点个数是 ( )
| A.至多为1 | B.2 | C.1 | D.0 |
已知椭圆 与双曲线
与双曲线 有相同的焦点
有相同的焦点 和
和 ,若
,若 是
是 的等比中项,
的等比中项,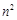 是
是 与
与 的等差中项,则椭圆的离心率是( )
的等差中项,则椭圆的离心率是( )
A. | B. | C. | D. |
当a为任意实数时,直线 恒过定点P,则过点P的抛物线的标准方程是( )
恒过定点P,则过点P的抛物线的标准方程是( )
A.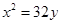 或 或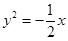 | B.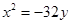 或 或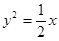 |
C.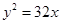 或 或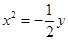  | D.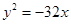 或 或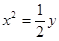 |
设斜率为2的直线l过双曲线 的右焦 点,且与双曲线的左、右两支分别相交,则双曲线离心率e的取值范围是( )
的右焦 点,且与双曲线的左、右两支分别相交,则双曲线离心率e的取值范围是( )
A.e> | B.e> | C.1<e< | D.1<e< |
已知a,b为正常数,F1,F2是两个定点,且|F1F2|=2a(a是正常数),动点P满足|PF1|+|PF2|=a2+1,则动点P的轨迹是( )
| A.椭圆 | B.线段 | C.椭圆或线段 | D.直线 |
椭圆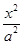 +
+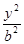 =1(a>b>0)的离心率是
=1(a>b>0)的离心率是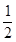 ,则
,则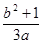 的最小值为( )
的最小值为( )
A.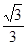 | B.1 | C.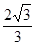 | D.2 |
 的左焦点
的左焦点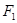 作斜率为1的直线,该直线与双曲线的两条渐近线的交点分别为A、B,若
作斜率为1的直线,该直线与双曲线的两条渐近线的交点分别为A、B,若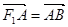 ,则双曲线的渐近线方程为( )
,则双曲线的渐近线方程为( )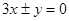 B.
B.
 D.
D.