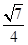题目内容
下列关于直线l,m与平面α,β的说法,正确的是 ( )
A.若l β且α⊥β,则l⊥α β且α⊥β,则l⊥α | B.若l⊥β且α∥β,则l⊥α |
| C.若l⊥β且α⊥β,则l∥α | D.若α β=m,且l∥m, 则l∥α β=m,且l∥m, 则l∥α |
B
解析试题分析:对于选项A,由于l β且α⊥β,则l⊥α,那么根据面面垂直的性质定理可知,只有垂直于交线是成立,对于C,由于l⊥β且α⊥β,则l∥α,可能l在平面α内,对于D,由于α
β且α⊥β,则l⊥α,那么根据面面垂直的性质定理可知,只有垂直于交线是成立,对于C,由于l⊥β且α⊥β,则l∥α,可能l在平面α内,对于D,由于α β=m,且l∥m, 则l∥α,根据线面平行的判定定理,只有m不在平面α内成立,故排除法选B.
β=m,且l∥m, 则l∥α,根据线面平行的判定定理,只有m不在平面α内成立,故排除法选B.
考点:空间中直线与面之间的位置关系,
点评:本题考查的知识点是空间中直线与面之间的位置关系,熟练掌握空间中线与面之间位置关系的定义及判定方法是解答本题的关键.

练习册系列答案
 期末宝典单元检测分类复习卷系列答案
期末宝典单元检测分类复习卷系列答案
相关题目
设m,n是不同的直线, 是不同的平面,下列命题中正确的是
是不同的平面,下列命题中正确的是
A.若m// |
B.若m// |
C.若m//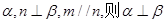 |
D.若m// |
平面 和直线
和直线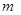 ,给出条件:①
,给出条件:① ;②
;② ;③
;③ ;④
;④ ;⑤
;⑤ .为使
.为使 ,应选择下面四个选项中的条件( )
,应选择下面四个选项中的条件( )
| A.①⑤ | B.①④ | C.②⑤ | D.③⑤ |
如图,在长方体 中,
中,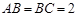 ,
, ,则异面直线
,则异面直线 与
与 所成的角为 ( )
所成的角为 ( )
A. | B.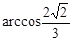 |
C.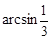 | D. |
两条异面直线所成角的范围是( )
A. | B. | C. | D. |
设、 是两条不同的直线,
是两条不同的直线, 是一个平面,则下列命题正确的是( )
是一个平面,则下列命题正确的是( )
A.若 , , ,则 ,则 | B.若 , , ,则 ,则 |
C.若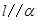 , , ,则 ,则 | D.若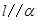 , , ,则 ,则 |
已知直线 ,平面
,平面 ,且
,且 ,给出四个命题: ①若
,给出四个命题: ①若 ∥
∥ ,则
,则 ;②若
;②若 ,则
,则 ∥
∥ ;③若
;③若 ,则
,则 ∥m;④若
∥m;④若 ∥m,则
∥m,则 .其中真命题的个数是
.其中真命题的个数是
| A.4 | B.3 | C.2 | D.1 |
已知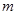 、
、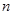 为两条不同的直线,
为两条不同的直线,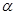 、
、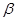 为两个不同的平面,则下列推理中正确的是( )
为两个不同的平面,则下列推理中正确的是( )
A.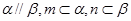 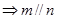 | B.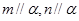 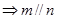 |
C.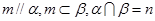 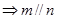 | D.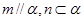 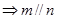 |
 的侧棱与底面边长都相等,
的侧棱与底面边长都相等,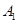 在底面
在底面 上的射影为
上的射影为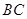 的中点D,则异面直线AD与
的中点D,则异面直线AD与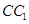 所成的角的余弦值为( )
所成的角的余弦值为( )