Question

【题目】已知是数列的前n项和，满足，正项等比数列的前n项和为，且满足.

(Ⅰ) 求数列{an}和{bn}的通项公式； (Ⅱ) 记，求数列{cn}的前n项和．

Answer 1

【答案】(Ⅰ) ，(Ⅱ) Gn＝n·2n＋1

【解析】

试题分析：（1）利用递推关系可得．利用等比数列的通项公式及其前n项和公式可得；（2）利用“错位相减法”与等比数列的前n项和公式即可得出

试题解析：(1)

--------------------------3分

设等比数列{bn}的公比为q，首项为，

依题意可知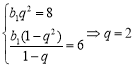或（舍）----5分

--------------------6分

(2) 则2×2＋3×22＋4×23＋…＋n×2n－1 ＋(n＋1)×2n，

22×22＋3×23＋…＋(n－1)×2n－1＋n×2n＋(n＋1)2n＋1，……8分

所以－Gn＝2×2＋(22＋23＋…＋2n)－(n＋1)×2n＋1,

即－Gn＝2×2＋－(n＋1)×2n＋1,--------------------10分

－Gn＝2×2＋－(n＋1)×2n＋1

－Gn＝－(n＋1)×2n＋1

－Gn＝－n×2n＋1

Gn＝n·2n＋1，n∈N*.----------------------------------------12分