题目内容
8.在极坐标系中,若点A、B的极坐标分别为(3,$\frac{π}{3}$),(-4,$\frac{7π}{6}$),则△AOB(O为极点)的面积等于3.分析 点B(-4,$\frac{7π}{6}$),即为$B(4,\frac{π}{6})$.利用S△AOB=$\frac{1}{2}|OA||OB|sin(\frac{π}{3}-\frac{π}{6})$即可得出.
解答 解:点B(-4,$\frac{7π}{6}$),即为$B(4,\frac{π}{6})$.
∴S△AOB=$\frac{1}{2}×3×4×sin(\frac{π}{3}-\frac{π}{6})$=3.
故答案为:3.
点评 本题考查了极坐标、三角形面积计算公式,考查了推理能力与计算能力,属于基础题.

练习册系列答案
相关题目
19.某射击运动员射击一次,命中目标的概率为0.8,问他连续射击两次都没命中的概率为( )
| A. | 0.8 | B. | 0.64 | C. | 0.16 | D. | 0.04 |
13.如图所示的程序框图,若输出的S是62,则①可以为( )
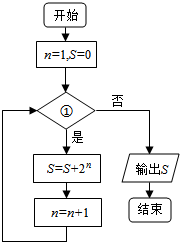

| A. | n≤3? | B. | n≤4? | C. | n≤5? | D. | n≤6? |
20.已知p:不等式|x+1|+|x-2|>m的解集为R;q:f(x)=log(5-2m)x为减函数,则p成立是q成立的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
18.若角α的终边经过点$(\sqrt{5},-2)$,则sinα等于多少( )
| A. | $\frac{2}{3}$ | B. | $\frac{{\sqrt{5}}}{3}$ | C. | $-\frac{2}{3}$ | D. | $-\frac{{\sqrt{5}}}{3}$ |