题目内容
【题目】设等差数列{an}的前n项和为Sn , 且a2=8,S4=40.数列{bn}的前n项和为Tn , 且Tn﹣2bn+3=0,n∈N* .
(Ⅰ)求数列{an},{bn}的通项公式;
(Ⅱ)设cn=![]() , 求数列{cn}的前n项和Pn .
, 求数列{cn}的前n项和Pn .
【答案】解:(Ⅰ)设等差数列{an}的公差为d,
由题意,得![]() ,
,
解得![]() ,
,
∴an=4n,
∵Tn﹣2bn+3=0,∴当n=1时,b1=3,当n≥2时,Tn﹣1﹣2bn﹣1+3=0,
两式相减,得bn=2bn﹣1 , (n≥2)
则数列{bn}为等比数列,
∴![]() ;
;
(Ⅱ)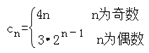 .
.
当n为偶数时,Pn=(a1+a3+…+an﹣1)+(b2+b4+…+bn)
=![]() .
.
当n为奇数时,
(法一)n﹣1为偶数,Pn=Pn﹣1+cn=2(n﹣1)+1+(n﹣1)2﹣2+4n=2n+n2+2n﹣1,
(法二)Pn=(a1+a3+…+an﹣2+an)+(b2+b4+…+bn﹣1)
=![]() .
.
∴![]() .
.
【解析】(Ⅰ)运用等差数列的通项公式与求和公式,根据条件列方程,求出首项和公差,得到通项an , 运用n=1时,b1=T1 , n>1时,bn=Tn﹣Tn﹣1 , 求出bn;
(Ⅱ)写出cn , 然后运用分组求和,一组为等差数列,一组为等比数列,分别应用求和公式化简即可.
【考点精析】解答此题的关键在于理解数列的前n项和的相关知识,掌握数列{an}的前n项和sn与通项an的关系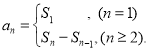 ,以及对等差数列的性质的理解,了解在等差数列{an}中,从第2项起,每一项是它相邻二项的等差中项;相隔等距离的项组成的数列是等差数列.
,以及对等差数列的性质的理解,了解在等差数列{an}中,从第2项起,每一项是它相邻二项的等差中项;相隔等距离的项组成的数列是等差数列.

练习册系列答案
 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案
相关题目