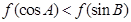题目内容
(本小题满分13分)
已知函数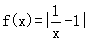
(Ⅰ)判断f(x)在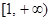 上的单调性,并证明你的结论;
上的单调性,并证明你的结论;
(Ⅱ)若集合A="{y" | y=f(x),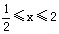 },B=[0,1], 试判断A与B的关系;
},B=[0,1], 试判断A与B的关系;
已知函数
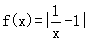
(Ⅰ)判断f(x)在
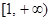 上的单调性,并证明你的结论;
上的单调性,并证明你的结论;(Ⅱ)若集合A="{y" | y=f(x),
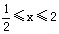 },B=[0,1], 试判断A与B的关系;
},B=[0,1], 试判断A与B的关系;解:(1)f(x)在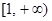 上为增函数.(2)A=B.
上为增函数.(2)A=B.
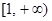 上为增函数.(2)A=B.
上为增函数.(2)A=B.本试题主要是考查了函数的单调性和集合的关系的运用
(1)先判定单调性,然后运用单调性定义法来证明得到结论。
(2)根据给定的集合,利用函数的 图像得到值域,进而判定集合A,B的关系。
解:(1)f(x)在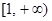 上为增函数.∵x≥1时,f(x)=1-
上为增函数.∵x≥1时,f(x)=1-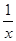 对任意的x1,x2,当1≤x1<x2时f(x1)- f(x2)=(1-
对任意的x1,x2,当1≤x1<x2时f(x1)- f(x2)=(1-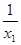 )-(1-
)-(1-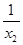 )=
)=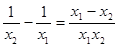 ∵x1x2>0,x1-x2<0 ∴
∵x1x2>0,x1-x2<0 ∴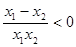 ∴f(x1)< f(x2)∴f(x)在
∴f(x1)< f(x2)∴f(x)在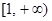 上为增函数.
上为增函数.
(2)证明f(x)在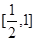 上单调递减,[1,2]上单调递增, 求出A=[0,1]说明A=B.
上单调递减,[1,2]上单调递增, 求出A=[0,1]说明A=B.
(1)先判定单调性,然后运用单调性定义法来证明得到结论。
(2)根据给定的集合,利用函数的 图像得到值域,进而判定集合A,B的关系。
解:(1)f(x)在
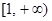 上为增函数.∵x≥1时,f(x)=1-
上为增函数.∵x≥1时,f(x)=1-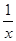 对任意的x1,x2,当1≤x1<x2时f(x1)- f(x2)=(1-
对任意的x1,x2,当1≤x1<x2时f(x1)- f(x2)=(1-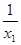 )-(1-
)-(1-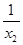 )=
)=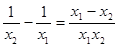 ∵x1x2>0,x1-x2<0 ∴
∵x1x2>0,x1-x2<0 ∴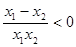 ∴f(x1)< f(x2)∴f(x)在
∴f(x1)< f(x2)∴f(x)在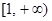 上为增函数.
上为增函数.(2)证明f(x)在
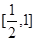 上单调递减,[1,2]上单调递增, 求出A=[0,1]说明A=B.
上单调递减,[1,2]上单调递增, 求出A=[0,1]说明A=B.
练习册系列答案
相关题目
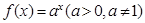 在
在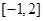 上的最大值为4,最小值为
上的最大值为4,最小值为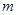 ,
,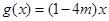 在R上是增函数,则
在R上是增函数,则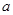 = .
= .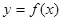 ,满足
,满足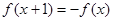 ,且在
,且在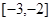 上是减函数,若
上是减函数,若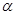 ,
,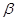 是锐角三角形的两个内角,则 ( )
是锐角三角形的两个内角,则 ( )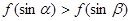


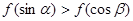
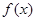 =
=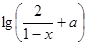 是奇函数,则
是奇函数,则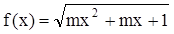 的定义域是一切实数,则m的取值范围是__________。
的定义域是一切实数,则m的取值范围是__________。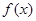 在
在 上有定义,对任意实数
上有定义,对任意实数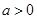 和任意实数
和任意实数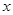 ,都有
,都有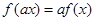 ,若
,若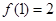 ,则函数
,则函数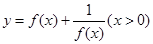 的递减区间是______.
的递减区间是______.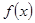 的定义域为
的定义域为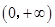 ,且满足条件:
,且满足条件: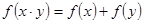 ,②
,②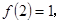 ③当
③当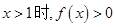
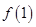 的值
的值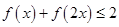 的x的取值范围。
的x的取值范围。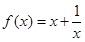 的单调递减区间是
的单调递减区间是
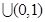
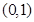
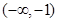 ,
,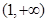
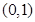 的函数
的函数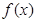 ,对于任意
,对于任意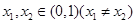 ,恒有
,恒有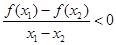 . 若A、B为锐角三角形ABC的两内角,则有( )
. 若A、B为锐角三角形ABC的两内角,则有( )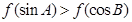 B、
B、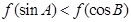
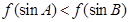 D、
D、