题目内容
(本小题14分)已知函数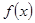 的定义域为
的定义域为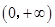 ,且满足条件:
,且满足条件:
①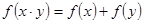 ,②
,②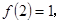 ③当
③当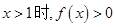
1)、求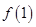 的值
的值
2)、讨论函数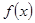 的单调性;
的单调性;
3)、求满足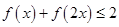 的x的取值范围。
的x的取值范围。
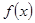 的定义域为
的定义域为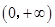 ,且满足条件:
,且满足条件:①
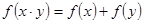 ,②
,②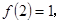 ③当
③当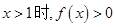
1)、求
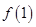 的值
的值2)、讨论函数
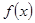 的单调性;
的单调性;3)、求满足
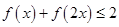 的x的取值范围。
的x的取值范围。1)f(1)="0" ; 2)f(x)在(0,+∞)上是增函数;3) .
.
 .
. 本试题主要是考查了函数的赋值法的运用,以及函数单调性的证明以及运用单调性解不等式的运用。
(1)令x="y=1," 得f(1)=" f" (1)+ f(1)故 f(1)=0,得到结论。
(2)在①中令 ,然后利用单调性
,然后利用单调性 得到函数是定义域内的增函数,
得到函数是定义域内的增函数,
(3)由
 ,由由2)知,f(x)在(0,+∞)上是增函数,得到关于x的不等式,求解得到。
,由由2)知,f(x)在(0,+∞)上是增函数,得到关于x的不等式,求解得到。
1)在①中令x="y=1," 得f(1)=" f" (1)+ f(1)故 f(1)=0 ……2分
2)在①中令 ……4分
……4分
先讨论 上的单调性, 任取x1 x2,设x2>x1>0,
上的单调性, 任取x1 x2,设x2>x1>0,
 ……分
……分
 ,由③知:
,由③知: >0,∴f(x2)>f(x1),
>0,∴f(x2)>f(x1),
∴f(x)在(0,+∞)上是增函数,……8分
3)由 ……9分
……9分
 , ……11分
, ……11分
又由2)知,f(x)在(0,+∞)上是增函数,故得:
 解得
解得 . ……14分
. ……14分
(1)令x="y=1," 得f(1)=" f" (1)+ f(1)故 f(1)=0,得到结论。
(2)在①中令
 ,然后利用单调性
,然后利用单调性 得到函数是定义域内的增函数,
得到函数是定义域内的增函数,(3)由

 ,由由2)知,f(x)在(0,+∞)上是增函数,得到关于x的不等式,求解得到。
,由由2)知,f(x)在(0,+∞)上是增函数,得到关于x的不等式,求解得到。1)在①中令x="y=1," 得f(1)=" f" (1)+ f(1)故 f(1)=0 ……2分
2)在①中令
 ……4分
……4分先讨论
 上的单调性, 任取x1 x2,设x2>x1>0,
上的单调性, 任取x1 x2,设x2>x1>0, ……分
……分 ,由③知:
,由③知: >0,∴f(x2)>f(x1),
>0,∴f(x2)>f(x1),∴f(x)在(0,+∞)上是增函数,……8分
3)由
 ……9分
……9分 , ……11分
, ……11分又由2)知,f(x)在(0,+∞)上是增函数,故得:
 解得
解得 . ……14分
. ……14分 
练习册系列答案
相关题目
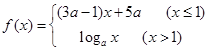 是在定义域上的单调递减函数,则
是在定义域上的单调递减函数,则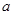 的取值范围为____ .
的取值范围为____ .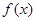 在
在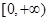 上是增函数,则满足
上是增函数,则满足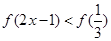 的
的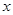 的取值范围是_____.
的取值范围是_____. 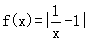
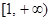 上的单调性,并证明你的结论;
上的单调性,并证明你的结论;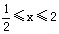 },B=[0,1], 试判断A与B的关系;
},B=[0,1], 试判断A与B的关系; ,则满足不等式
,则满足不等式 的
的 的取值范围
的取值范围



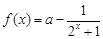 ,
,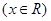 .
.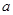 为何实数
为何实数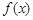 在
在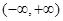 上为增函数;
上为增函数; 在
在 上是增函数,且最小值是1,则它在
上是增函数,且最小值是1,则它在 上是( )
上是( )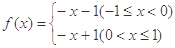 ,则
,则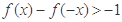 的解集为( )
的解集为( ) )∪(0,1]
)∪(0,1]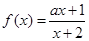 在区间
在区间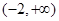 上是增函数,则
上是增函数,则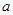 的取值范围是 .
的取值范围是 .