题目内容
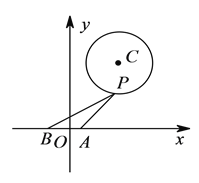
【题目】如图,在平面直角坐标系内,已知点A(1,0,B(-1,0),圆![]() 的方程为
的方程为![]() ,点
,点![]() 为圆上的动点.
为圆上的动点.
(1)求过点![]() 的圆
的圆![]() 的切线方程.
的切线方程.
(2)求![]() 的最大值及此时对应的点
的最大值及此时对应的点![]() 的坐标.
的坐标.
【答案】(1)3x-4y-3=0或x=1;(2)详见解析.
【解析】试题分析: (![]() )当
)当![]() 存在时,设过点
存在时,设过点![]() 切线的方程为
切线的方程为![]() ,由圆心到直线的距离等于半径列出方程,求出k值,即可得到切线方程; 当
,由圆心到直线的距离等于半径列出方程,求出k值,即可得到切线方程; 当![]() 不存在时方程
不存在时方程![]() 也满足;(2) 设点
也满足;(2) 设点![]() ,则由两点之间的距离公式知
,则由两点之间的距离公式知![]() ,即所求的最大值可转化为
,即所求的最大值可转化为![]() 最大值, 又
最大值, 又![]() 为圆上点,所以
为圆上点,所以![]() ,再联立此时的直线OC与圆方程求出对应的P点坐标.
,再联立此时的直线OC与圆方程求出对应的P点坐标.
试题解析:(1) 当![]() 存在时,设过点
存在时,设过点![]() 切线的方程为
切线的方程为![]() ,
,
∵圆心坐标为![]() ,半径
,半径![]() ,∴
,∴![]() ,计算得出
,计算得出![]() ,
,
∴所求的切线方程为![]() ; 当
; 当![]() 不存在时方程
不存在时方程![]() 也满足,综上所述,所求的直线方程为
也满足,综上所述,所求的直线方程为![]() 或
或![]() 。
。
(![]() )设点
)设点![]() ,则由两点之间的距离公式知
,则由两点之间的距离公式知
![]() ,
,
要![]() 取得最大值只要使
取得最大值只要使![]() 最大即可,
最大即可,
又![]() 为圆上点,所以
为圆上点,所以![]() ,
,
∴![]() ,
,
此时直线![]() ,由
,由 ,计算得出
,计算得出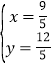 (舍去)或
(舍去)或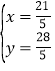 ,∴点
,∴点![]() 的坐标为
的坐标为![]() .
.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目

