题目内容
【题目】一条光线经过P(2,3)点,射在直线l:x+y+1=0上,反射后穿过点Q(1,1).
(1)求入射光线的方程;
(2)求这条光线从P到Q的长度.

【答案】(1) 5x-4y+2=0. (2) ![]()
【解析】试题分析:(1)设点Q′(x′,y′)为Q关于直线l的对称点且QQ′交l于M点,可得直线QM的方程,与l联立可得点M的坐标,利用中点坐标公式可得Q′的坐标.设入射线与l交于点N,利用P,N,Q′共线,得到入射光线PN的方程;
(2)利用两点间的距离公式求出PQ′即可.
试题解析:
(1)设点Q′(x′,y′)为Q关于直线l的对称点且QQ′交l于M点.
∵![]() ,∴kQQ′=1.
,∴kQQ′=1.
∴QQ′所在直线方程为y-1=1·(x-1),
即x-y=0.
由![]()
解得l与QQ′的交点M的坐标为![]() .
.
又∵M为QQ′的中点,
由此得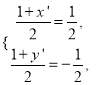 解得
解得![]()
∴Q′(-2,-2).
设入射光线与l交点为N,则P、N、Q′共线.
又P(2,3),Q′(-2,-2),得入射光线的方程为![]() ,
,
即5x-4y+2=0.
(2)∵l是QQ′的垂直平分线,从而|NQ|=|NQ′|,
∴|PN|+|NQ|=|PN|+|NQ′|=|PQ′|=![]() ,
,
即这条光线从P到Q的长度是![]() .
.

练习册系列答案
 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案
相关题目