Question

【题目】已知函数f(x)的定义域为(－2,2)，函数g(x)＝f(x－1)＋f(3－2x)．

(1)求函数g(x)的定义域；

(2)若f(x)是奇函数，且在定义域上单调递减，求不等式g(x)≤0的解集．

Answer 1

【答案】（1）；（2）．

【解析】

试题分析：（1）由题意知，，解此不等式组得出函数g（x）的定义域．

（2）等式g（x）≤0，即 f（x﹣1）≤﹣f（3﹣2x）=f（2x﹣3），有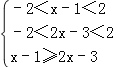，解此不等式组，

可得结果．

解：（1）∵数f（x）的定义域为（﹣2，2），函数g（x）=f（x﹣1）+f（3﹣2x）．

∴，∴＜x＜，函数g（x）的定义域（，）．

（2）∵f（x）是奇函数且在定义域内单调递减，不等式g（x）≤0，

∴f（x﹣1）≤﹣f（3﹣2x）=f（2x﹣3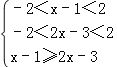），∴，∴＜x≤2，

故不等式g（x）≤0的解集是 （，2]．