Question

【题目】已知焦距为2的椭圆W： =1（a＞b＞0）的左、右焦点分别为A1 ， A2 ， 上、下顶点分别为B1 ， B2 ， 点M（x0 ， y0）为椭圆W上不在坐标轴上的任意一点，且四条直线MA1 ， MA2 ， MB1 ， MB2的斜率之积为 ．

（1）求椭圆W的标准方程；
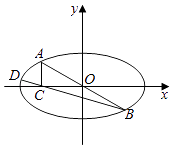
（2）如图所示，点A，D是椭圆W上两点，点A与点B关于原点对称，AD⊥AB，点C在x轴上，且AC与x轴垂直，求证：B，C，D三点共线．

Answer 1

【答案】
（1）

解：由题意可知：2c=2，c=1，a2﹣b2=1，

∵M（x0，y0）为椭圆W上不在坐标轴上的任意一点，

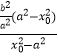
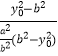∴ ， = （a2﹣ ）， = （b2﹣ ），

= = ，

= =（ ）2= ，则a2=2b2，

∴a2=2，b2=1，

∴椭圆W的标准方程

（2）

解：证明：不妨设点A（x1，y1），D（x2，y2），B的坐标（﹣x1，﹣y1），C（x1，0），

∵A，D在椭圆上， ，=0，即（x1﹣x2）（x1+x2）+2（y1﹣y2）（y1+y2）=0，

∴ =﹣ ，

由AD⊥AB，

∴kADkAB=﹣1， =﹣1， （﹣ ，）=﹣1，

∴ = ，

∴kBD﹣kBC= ﹣ = ﹣ =0，

kBD=kBC，

∴B，C，D三点共线

【解析】（1）由c=1，a2﹣b2=1，求得四条直线的斜率，由斜率乘积为 ，代入求得a和b的关系，即可求得a和b的值，求得椭圆W的标准方程；（2）设A，D的坐标，代入椭圆方程，作差法，求得直线AD的斜率，由kADkAB=﹣1，代入求得 = ，由kBD﹣kBC=0，即可求证kBD=kBC ， 即可求证B，C，D三点共线．