题目内容
设函数
(1)试问函数能否在处取得极值,请说明理由;
(2)若,当时,函数的图像有两个公共点,求的取值范围.
(1)试问函数能否在处取得极值,请说明理由;
(2)若,当时,函数的图像有两个公共点,求的取值范围.
(1)函数不能在处取得极值,理由详见试题解析;
(2)的取值范围是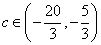 .
.
(2)的取值范围是
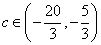 .
.试题分析:(1)先对函数求导,因为函数
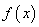 在实数
在实数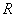 上单调递增,故函数不可再
上单调递增,故函数不可再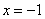 处取得极值.
处取得极值.(2)函数
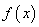 与
与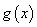 的图像在
的图像在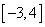 有两个公共点,即方程
有两个公共点,即方程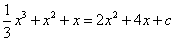 在
在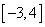 有两解,结合函数的单调性可求的取值范围.
有两解,结合函数的单调性可求的取值范围.(1)
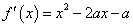 ,当
,当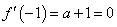 时,
时,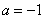 ,
,而此时
 ,函数
,函数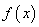 在实数
在实数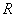 上单调递增,故函数不可再
上单调递增,故函数不可再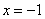 处取得极值.
处取得极值.(2)当
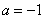 时,
时,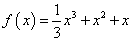 ,函数
,函数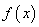 与
与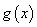 的图像在
的图像在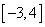 有两个公共点,即方程
有两个公共点,即方程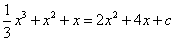 在
在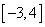 有两解,
有两解,方程可转化为
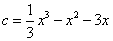 ,设
,设 ,
,则
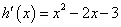 ,令
,令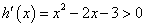 ,
,解得
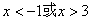 ,所以
,所以 函数在
函数在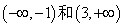 递增,在
递增,在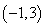 上递减.
上递减.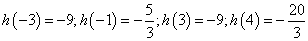 ,所以要使得方程有两解需
,所以要使得方程有两解需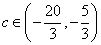 .
.
练习册系列答案
相关题目
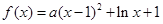 .
.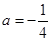 时,求函数
时,求函数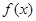 的极值;
的极值;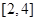 上是减函数,求实数
上是减函数,求实数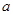 的取值范围;
的取值范围;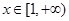 时,函数
时,函数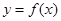 图像上的点都在
图像上的点都在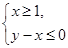 所表示的平面区域内,求实数
所表示的平面区域内,求实数 是可导的函数,且
是可导的函数,且 对于
对于 恒成立,则( )
恒成立,则( )
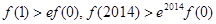


 (
( )的图像如图所示,则不等式
)的图像如图所示,则不等式 的解集为________.
的解集为________.
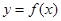 的导函数的图像,现有四种说法:
的导函数的图像,现有四种说法:
 在
在 上是增函数;
上是增函数;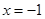 是
是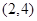 上是减函数,在
上是减函数,在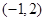 上是增函数;
上是增函数;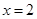 是
是
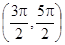


 的导函数为
的导函数为 ,若
,若 ,则
,则 .
.