题目内容
【题目】如图,在四棱锥![]() 中,
中,![]() ,
,![]() ,
,![]() 平面
平面![]() ,点
,点![]() 在棱
在棱![]() 上.
上.
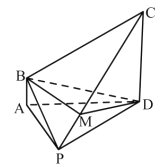
(Ⅰ)求证:平面![]() 平面
平面![]() ;
;
(Ⅱ)若直线![]() 平面
平面![]() ,求此时三棱锥
,求此时三棱锥![]() 的体积.
的体积.
【答案】(Ⅰ)详见解析;(Ⅱ)![]() .
.
【解析】
(I)先利用正弦定理以及三角形内角和定理证明![]() ,结合
,结合![]() 可得
可得![]() 平面
平面![]() ,由此能证明平面
,由此能证明平面![]() 平面
平面![]() ;(II)连结
;(II)连结![]() 与
与![]() 交于点
交于点![]() ,连结
,连结![]() ,可证明
,可证明![]() ,由
,由![]() =
=![]() ,由此能求出三棱推
,由此能求出三棱推![]() 的体积.
的体积.
(Ⅰ)因为AB⊥平面PAD,
所以AB⊥DP,
又因为![]() ,AP=2,∠PAD=60°,
,AP=2,∠PAD=60°,
由![]() ,可得
,可得![]() ,所以∠PDA=30°,
,所以∠PDA=30°,
所以∠APD=90°,即DP⊥AP,
因为![]() ,所以DP⊥平面PAB,
,所以DP⊥平面PAB,
因为![]() ,所以平面PAB⊥平面PCD
,所以平面PAB⊥平面PCD
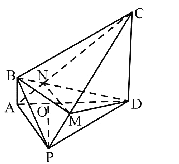
(Ⅱ)连结AC,与BD交于点N,连结MN,因为PA//平面MBD,
MN为平面PAC与平面MBD的交线,所以PA//MN,
所以![]() ,
,
在四边形ABCD中,因为AB//CD,所以![]() ,
,
所以![]() ,
,![]() ,
,![]() .
.
因为AB⊥平面PAD,所以AB⊥AD,且平面APD⊥平面ABCD,
在平面PAD中,作PO⊥AD,则PO⊥平面ABCD,
因为![]() ,
,
所以![]()
因为CD=3.所以![]() ,
,
所以![]() .
.

练习册系列答案
相关题目
【题目】2020年寒假,因为“新冠”疫情全体学生只能在家进行网上学习,为了研究学生网上学习的情况,某学校随机抽取![]() 名学生对线上教学进行调查,其中男生与女生的人数之比为
名学生对线上教学进行调查,其中男生与女生的人数之比为![]() ,抽取的学生中男生有
,抽取的学生中男生有![]() 人对线上教学满意,女生中有
人对线上教学满意,女生中有![]() 名表示对线上教学不满意.
名表示对线上教学不满意.
(1)完成![]() 列联表,并回答能否有
列联表,并回答能否有![]() 的把握认为“对线上教学是否满意 与性别有关”;
的把握认为“对线上教学是否满意 与性别有关”;
态度 性别 | 满意 | 不满意 | 合计 |
男生 | |||
女生 | |||
合计 | 100 |
(2)从被调查的对线上教学满意的学生中,利用分层抽样抽取![]() 名学生,再在这
名学生,再在这![]() 名学生中抽取
名学生中抽取![]() 名学生,作线上学习的经验介绍,求其中抽取一名男生与一名女生的概率.
名学生,作线上学习的经验介绍,求其中抽取一名男生与一名女生的概率.
附: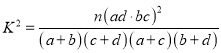 .
.
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
