题目内容
【题目】选修4-4：坐标系与参数方程
已知直线
的参数方程为
（
为参数）.以坐标原点为极点，
轴的正半轴为极轴建立极坐标系，曲线
的极坐标方程为
.
（1）求曲线的直角坐标方程；
（2）已知点
，直线与曲线交于
两点，且
，求
的值.
【答案】（1）
；（2）
【解析】
（1）由曲线
的极坐标方程得
，利用
可得曲线的直角坐标方程；（2）由直线
的参数方程化为普通方程得
，再求得直线的参数方程为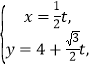
（
为参数），代入
，整理得
，利用韦达定理以及直线参数方程的几何意义可得结果.
（1）由曲线的极坐标方程得.
∵
∴曲线的直角坐标方程为.
（2）由直线的参数方程为
（为参数），化为普通方程得.
∵
在直线上
∴直线的参数方程可设为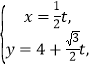（为参数），代入，整理得
，设
两点对应的参数分别为
，
，则
，∵
，∴
(a>0)，∴
.
故
的值为.
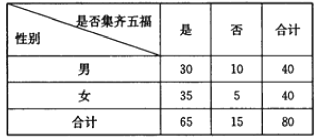
名校课堂系列答案
【题目】利用独立性检验的方法调查高中生性别与爱好某项运动是否有关，通过随机调查200名高中生是否爱好某项运动，利用
列联表，由计算可得
，参照下表：
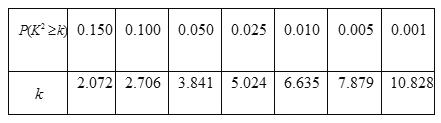
| 0.01 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.706 | 3.841 | 5,024 | 6.635 | 7.879 | 10.828 |
得到的正确结论是（ ）
A. 有99%以上的把握认为“爱好该项运动与性别无关”
B. 有99%以上的把握认为“爱好该项运动与性别有关”
C. 在犯错误的概率不超过0.5%的前提下，认为“爱好该项运动与性别有关”
D. 在犯错误的概率不超过0.5%的前提下，认为“爱好该项运动与性别无关”
【题目】某企业三月中旬生产A、B、C三种产品共3 000件，根据分层抽样的结果，企业统计员制作了如下的统计表格：
产品类别 | A | B | C |
产品数量（件） | 1 300 | ||
样本容量（件） | 130 |
由于不小心，表格中A、C产品的有关数据已被污染看不清楚，统计员记得A产品的样本容量比C产品的样本容量多10，根据以上信息，可得C的产品数量是（ ）
A.80B.800C.90D.900
