题目内容
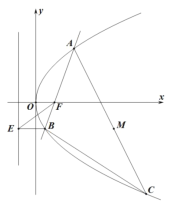
【题目】已知椭圆![]() 的左、右焦点分别为
的左、右焦点分别为![]() ,
,![]() ,点
,点![]() 在椭圆
在椭圆![]() 上,点
上,点![]() 满足以
满足以![]() 为直径的圆过椭圆的上顶点
为直径的圆过椭圆的上顶点![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)已知直线![]() 过右焦点
过右焦点![]() 与椭圆
与椭圆![]() 交于
交于![]() 两点,在
两点,在![]() 轴上是否存在点
轴上是否存在点![]() 使得
使得![]() 为定值?如果存在,求出点
为定值?如果存在,求出点![]() 的坐标;如果不存在,说明理由.
的坐标;如果不存在,说明理由.
【答案】(1)![]() ;(2)存在,
;(2)存在,![]()
【解析】
(1)由点在椭圆上代入可得![]() ,
,![]() 的关系,再由点
的关系,再由点![]() 满足以
满足以![]() 为直径的圆过椭圆的上顶点
为直径的圆过椭圆的上顶点![]() .可得
.可得![]() 可得
可得![]() ,
,![]() 的关系,再由
的关系,再由![]() ,
,![]() ,
,![]() 的关系求出椭圆的方程;
的关系求出椭圆的方程;
(2)由(1)可得右焦点![]() 的坐标,分坐标
的坐标,分坐标![]() 的斜率为0和不为0两种情况讨论,假设存在
的斜率为0和不为0两种情况讨论,假设存在![]() 满足条件,设直线
满足条件,设直线![]() 的方程,与椭圆联立求出两根之和及两根之积,进而求出数量积
的方程,与椭圆联立求出两根之和及两根之积,进而求出数量积![]() 的表达式,要使数量积为定值,则分子分母对应项的系数成比例,可得
的表达式,要使数量积为定值,则分子分母对应项的系数成比例,可得![]() 的值,且可求出定值.
的值,且可求出定值.
解:(1)由题意可得上顶点![]() ,
,![]() ,所以:
,所以:![]() ,
,![]() ,即
,即![]() ,
,![]() ,
,![]() 即
即![]() ,
,![]() ,
,
解得:![]() ,
,![]() ,
,
所以椭圆的方程为:![]() ;
;
(2)由(1)可得右焦点![]() 的坐标
的坐标![]() ,假设存在
,假设存在![]()
![]() 当直线
当直线![]() 的斜率不为0时,设直线
的斜率不为0时,设直线![]() 的方程为:
的方程为:![]() ,设
,设![]() ,
,![]() ,
,![]() ,
,![]() ,
,
联立直线与椭圆的方程![]() ,整理可得:
,整理可得:![]() ,
,![]() ,
,![]() ,
,
![]() ,
,![]() ,
,
因为![]()
![]() ,
,
要使![]() 为定值,则
为定值,则![]() ,解得:
,解得:![]() ,这时
,这时![]() 为定值,
为定值,
![]() 当直线
当直线![]() 的斜率为0时,则
的斜率为0时,则![]() ,
,![]() ,
,![]() 为
为![]() ,
,![]() ,则
,则![]() ,
,![]() ,
,![]() ,
,
综上所述:所以存在![]() ,
,![]() ,使
,使![]() 为定值.
为定值.

 名师点拨卷系列答案
名师点拨卷系列答案【题目】随着5G商用进程的不断加快,手机厂商之间围绕5G用户的争夺越来越激烈,5G手机也频频降低身价飞人寻常百姓家.某科技公司为了给自己新推出的5G手机定价,随机抽取了100人进行调查,对其在下一次更换5G手机时,能接受的价格(单位:元)进行了统计,得到结果如下表,已知这100个人能接受的价格都在![]() 之间,并且能接受的价格的平均值为2350元(同一组的数据用该组区间的中点值代替).
之间,并且能接受的价格的平均值为2350元(同一组的数据用该组区间的中点值代替).
分组 | 一 | 二 | 三 | 四 | 五 |
手机价格X(元) |
|
|
|
|
|
频数 | 10 | x | y | 20 | 20 |
(1)现用分层抽样的方法从第一、二、三组中随机抽取6人,将该样本看成一个总体,从中随机抽取2人,求其中恰有1人能接受的价格不低于2000元的概率;
(2)若人们对5G手机能接受的价格X近似服从正态分布![]() ,其中
,其中![]() 为样本平均数
为样本平均数![]() ,
,![]() 为样本方差
为样本方差![]() ,求
,求![]() .
.
附:![]() .若
.若![]() ,则
,则![]() ,
,![]() .
.
【题目】2019年2月13日《西安市全民阅读促进条例》全文发布,旨在保障全民阅读权利,培养全民阅读习惯,提高全民阅读能力,推动文明城市和文化强市建设.某高校为了解条例发布以来全校学生的阅读情况,随机调查了200名学生每周阅读时间![]() (单位:小时)并绘制如图所示的频率分布直方图.
(单位:小时)并绘制如图所示的频率分布直方图.
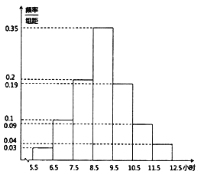
(1)求这200名学生每周阅读时间的样本平均数;
(2)为查找影响学生阅读时间的因素,学校团委决定从每周阅读时间为![]() ,
,![]() 的学生中抽取9名参加座谈会.
的学生中抽取9名参加座谈会.
(i)你认为9个名额应该怎么分配?并说明理由;
(ii)座谈中发现9名学生中理工类专业的较多.请根据200名学生的调研数据,填写下面的![]() 列联表,并判断是否有
列联表,并判断是否有![]() 的把握认为学生阅读时间不足(每周阅读时间不足8.5小时)与“是否理工类专业”有关?(精确到0.1)
的把握认为学生阅读时间不足(每周阅读时间不足8.5小时)与“是否理工类专业”有关?(精确到0.1)
阅读时间不足8.5小时 | 阅读时间超过8.5小时 | |
理工类专业 | 40 | 60 |
非理工类专业 |
附: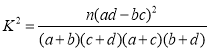 (
(![]() ).
).
临界值表:
| 0.150 | 0.100 | 0.050 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |