题目内容
9．如图，若函数y=f（x）的图象如图所示，则它的解析式为f（x）=$\left\{\begin{array}{l}{-x，x＜0}\\{2x，0≤x≤1}\\{2，x＞1}\end{array}\right.$．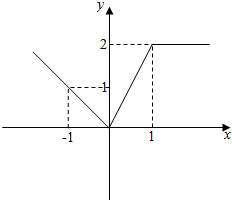
分析 分段求出函数的表达式，即可得出结论．
解答 解：由题意，x＜0时，直线的斜率为-1，方程为y=-x，
0≤x≤1时，直线的斜率为2，方程为y=2x，
x＞1时，方程为y=2．
∴f（x）=$\left\{\begin{array}{l}{-x，x＜0}\\{2x，0≤x≤1}\\{2，x＞1}\end{array}\right.$．
故答案为：f（x）=$\left\{\begin{array}{l}{-x，x＜0}\\{2x，0≤x≤1}\\{2，x＞1}\end{array}\right.$．
点评 本题考查函数的解析式，考查学生的计算能力，比较基础．
练习册系列答案
相关题目