题目内容
14.直线$\sqrt{3}$x-y+$\sqrt{6}$=0的倾斜角为$\frac{π}{3}$.分析 由直线方程求出直线的斜率,再由斜率是倾斜角的正切值得答案.
解答 解:由直线方程$\sqrt{3}$x-y+$\sqrt{6}$=0,的直线的斜率k=$\sqrt{3}$,
设直线的倾斜角为θ(0≤θ<π),
则tan$θ=\sqrt{3}$,∴$θ=\frac{π}{3}$.
故答案为:$\frac{π}{3}$.
点评 本题考查直线的倾斜角,考查直线倾斜角和斜率的关系,是基础题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
19.若曲线f(x)=$\frac{1}{3}$ax3+$\frac{1}{2}$bx2+cx+d(a,b,c>0)上不存在斜率为0的切线,则$\frac{f′(1)}{b}$-1的取值范围是( )
| A. | (1,+∞) | B. | [1,+∞) | C. | (2,+∞) | D. | [2,+∞) |
6.已知集合P={x|x2-x-2≤0},Q={x|log2(x-1)≤1},则P∩Q=( )
| A. | (-1,3) | B. | [-1,3) | C. | (1,2] | D. | [1,2] |

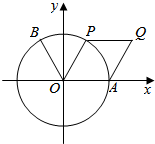 如图,点B(-$\frac{1}{2}$,$\frac{\sqrt{3}}{2}$),点A时单位圆与x轴正半轴的交点.设点P为单位圆上的动点,点Q满足$\overrightarrow{OQ}$=$\overrightarrow{OA}$+$\overrightarrow{OP}$,∠AOP=2θ($\frac{π}{6}$≤θ<$\frac{π}{2}$),f(θ)=$\overrightarrow{OB}$•$\overrightarrow{OQ}$,求f(θ)的取值范围,当$\overrightarrow{OB}$⊥$\overrightarrow{OQ}$时,求四边形OAQP的面积.
如图,点B(-$\frac{1}{2}$,$\frac{\sqrt{3}}{2}$),点A时单位圆与x轴正半轴的交点.设点P为单位圆上的动点,点Q满足$\overrightarrow{OQ}$=$\overrightarrow{OA}$+$\overrightarrow{OP}$,∠AOP=2θ($\frac{π}{6}$≤θ<$\frac{π}{2}$),f(θ)=$\overrightarrow{OB}$•$\overrightarrow{OQ}$,求f(θ)的取值范围,当$\overrightarrow{OB}$⊥$\overrightarrow{OQ}$时,求四边形OAQP的面积.