题目内容
将红、黄、绿、黑四种不同的颜色涂入如图中的五个区域内,要求相邻的两个区域的颜色都不相同,则有多少种不同的涂色方法?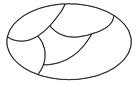
72(种)
解析解:给区域标记号A、B、C、D、E(如图所示),则A区域有4种不同的涂色方法,B区域有3种,C区域有2种,D区域有2种,但E区域的涂色依赖于B与D涂色的颜色,如果B与D颜色相同有2种涂色方法,不相同,则只有一种.因此应先分类后分步.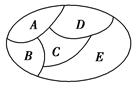
(1)当B与D同色时,有4×3×2×1×2=48(种).
(2)当B与D不同色时,有4×3×2×1×1=24(种).
故共有48+24=72(种)不同的涂色方法.

练习册系列答案
 名校名师培优作业本加核心试卷系列答案
名校名师培优作业本加核心试卷系列答案 全程金卷系列答案
全程金卷系列答案
相关题目
 展开式中的所有二项式系数和为512,
展开式中的所有二项式系数和为512, 的展开式中,某一项的系数是它前一项系数的2倍,而又等于它后一项系数的
的展开式中,某一项的系数是它前一项系数的2倍,而又等于它后一项系数的
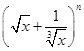 的展开式的二项式系数之和比(a+b)2n的展开式的系数之和小240,求
的展开式的二项式系数之和比(a+b)2n的展开式的系数之和小240,求