题目内容
已知 的展开式中,某一项的系数是它前一项系数的2倍,而又等于它后一项系数的
的展开式中,某一项的系数是它前一项系数的2倍,而又等于它后一项系数的
(Ⅰ)求展开后所有项的系数之和及所有项的二项式系数之和;
(Ⅱ)求展开式中的有理项.
(Ⅰ)所有项的二项式系数和为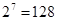 .
.
(Ⅱ)有理项为: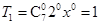 ,
,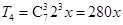 ,
,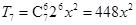 .
.
解析试题分析:根据题意,设该项为第r+1项,则有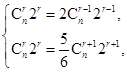 3分
3分
即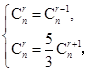 亦即
亦即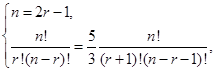
解得 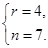 6分
6分
(Ⅰ)令x=1得展开式中所有项的系数和为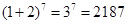 .
.
所有项的二项式系数和为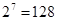 . 8分
. 8分
(Ⅱ)展开式的通项为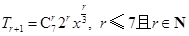 .
.
于是当r=0,3, 6时,对应项为有理项, 11分
即有理项为: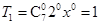 ,
,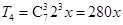 ,
,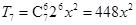 .14分
.14分
考点:本题主要考查二项式展开式的通项公式,二项式系数的性质。
点评:典型题,本题全面考查二项式定理的相关内容,对组合数公式的应用及复杂式子的变形能力要求较高。

练习册系列答案
相关题目
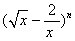 的展开式中:
的展开式中: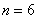 ,求倒数第二项
,求倒数第二项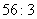 ,求各项的二项式系数和。
,求各项的二项式系数和。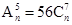 ,且(1-2x)n=a0+a1x+a2x2+a3x3+……+anxn.
,且(1-2x)n=a0+a1x+a2x2+a3x3+……+anxn.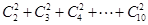
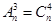 ,求n.
,求n.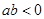 且
且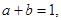 二项式
二项式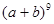 按
按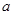 的降幂排列,展开后其第二项不大于第三项,求
的降幂排列,展开后其第二项不大于第三项,求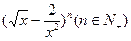 的二项
的二项 展开式中第五项的系数与第三项的系数的比是10:1.
展开式中第五项的系数与第三项的系数的比是10:1. 展开式中各项系数的和;
展开式中各项系数的和;