题目内容
7名同学排队照相.
(1)若分成两排照,前排3人,后排4人,有多少种不同的排法?
(2)若排成两排照,前排3人,后排4人,但其中甲必须在前排,乙必须在后排,有多少种不同的排法?
(3)若排成一排照,甲、乙、丙三人必须相邻,有多少种不同的排法?
(4)若排成一排照,7人中有4名男生,3名女生,女生不能相邻,有多少种不同的排法?
(1)5040 (2)1440 (3)720 (4)1440
解析解:(1)A73·A44=A77=5040(种).
(2)第一步安排甲,有A31种排法;第二步安排乙,有A41种排法;第三步余下的5人排在剩下的5个位置上,有A55种排法.由分步计数原理得,符合要求的排法共有
A31·A41·A55=1440(种).
(3)第一步,将甲、乙、丙视为一个元素,与其余4个元素排成一排,即看成5个元素的全排列问题,有A55种排法;第二步,甲、乙、丙三人内部全排列,有A33种排法.由分步计数原理得,共有A55·A=720(种).
(4)第一步,4名男生全排列,有A44种排法;第二步,女生插空,即将3名女生插入4名男生之间的5个空位,这样可保证女生不相邻,有A53种插入方法.由分步计数原理得,符合条件的排法共有A44·A53=1440(种).

练习册系列答案
相关题目
 -
-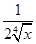 )n的展开式中,前三项系数的绝对值依次成等差数列.
)n的展开式中,前三项系数的绝对值依次成等差数列.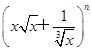 的展开式奇数项的二项式系数之和为128,求展开式中二项式系数最大项.
的展开式奇数项的二项式系数之和为128,求展开式中二项式系数最大项.
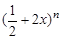 的展开式中,
的展开式中,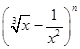 的展开式的二项式系数和为128.
的展开式的二项式系数和为128.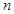 的值;
的值; 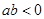 且
且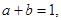 二项式
二项式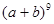 按
按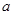 的降幂排列,展开后其第二项不大于第三项,求
的降幂排列,展开后其第二项不大于第三项,求