题目内容
设集合I={1,2,3,4,5}.选择I的两个非空子集A和B,求使B中最小的数大于A中最大的数的不同选择方法有多少种?
49
解析解:当A中最大的数为1时,B可以是{2,3,4,5}的非空子集,有24-1=15(种)选择方法;
当A中最大的数为2时,A可以是{2}或{1,2},B可以是{3,4,5}的非空子集,有2×(23-1)=14种选择方法;
当A中最大的数为3时,A可以是{3,},{1,3},{2,3}或{1,2,3},B可以是{4,5}的非空子集,有4×(22-1)=12(种)选择方法;
当A中最大的数为4时,A可以是{4},{1,4},{2,4},{3,4},{1,2,4},{1,3,4},{2,,3,4}或{1,2,3,4},B可以是{5},有8×1=8(种)选择方法.
所以满足条件的非空子集共有15+14+12+8=49(种)不同的选择方法.

练习册系列答案
相关题目
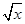 )n的展开式中,某一项的系数恰好是它前一项系数的2倍,而且是它后一项系数的
)n的展开式中,某一项的系数恰好是它前一项系数的2倍,而且是它后一项系数的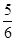 ,求展开式中二项式系数最大的项.
,求展开式中二项式系数最大的项.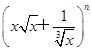 的展开式奇数项的二项式系数之和为128,求展开式中二项式系数最大项.
的展开式奇数项的二项式系数之和为128,求展开式中二项式系数最大项.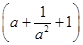 10展开式中的常数项.
10展开式中的常数项.
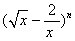 的展开式中:
的展开式中: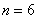 ,求倒数第二项
,求倒数第二项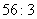 ,求各项的二项式系数和。
,求各项的二项式系数和。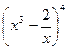 的展开式中的常数项等于 ;
的展开式中的常数项等于 ;