题目内容
【题目】以下关于线性回归的判断,正确的个数是( )

①若散点图中所有点都在一条直线附近,则这条直线为回归直线;
②散点图中的绝大多数都线性相关,个别特殊点不影响线性回归,如图中的A,B,C点;
③已知直线方程为![]() =0.50x-0.81,则x=25时,y的估计值为11.69;
=0.50x-0.81,则x=25时,y的估计值为11.69;
④回归直线方程的意义是它反映了样本整体的变化趋势.
A. 0 B. 1 C. 2 D. 3
【答案】D
【解析】
利用线性回归方程的概念及意义对①②③④四个选项逐一判断即可.
能使所有数据点都在一条直线附近的直线不止一条,而回归方程的定义知,只有按最小二乘法求得回归系数a,b得到的直线![]() =ax+b才是回归方程,
=ax+b才是回归方程,
∴①不对;
②散点图中的绝大多数点都线性相关,个别特殊点不会影响线性回归,是正确,故②正确;
③将x=25代入![]() =0.50x﹣0.81,解得
=0.50x﹣0.81,解得![]() =11.69,
=11.69,
∴③正确;
④散点图中所有点都在回归直线的附近,因此回归直线方程反映了样本整体的变化趋势,故④正确;
综上所述,正确的有3个.
故选:D.

 名校课堂系列答案
名校课堂系列答案【题目】为了监控某种零件的一条生产线的生产过程,检验员每隔30 min从该生产线上随机抽取一个零件,并测量其尺寸(单位:cm).下面是检验员在一天内依次抽取的16个零件的尺寸:
抽取顺序 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
零件尺寸 | 9.95 | 10.12 | 9.96 | 9.96 | 10.01 | 9.92 | 9.98 | 10.04 |
抽取次序 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 |
零件尺寸 | 10.26 | 9.91 | 10.13 | 10.02 | 9.22 | 10.04 | 10.05 | 9.95 |
经计算得![]() =
=![]() xi=9.97,s=
xi=9.97,s=![]() =
=![]() ≈0.212,
≈0.212,![]() ≈18.439,
≈18.439,![]() (xi﹣
(xi﹣![]() )(i﹣8.5)=﹣2.78,
)(i﹣8.5)=﹣2.78,
其中xi为抽取的第i个零件的尺寸,i=1,2,…,16.
(1)求(xi,i)(i=1,2,…,16)的相关系数r,并回答是否可以认为这一天生产的零件尺寸不随生产
过程的进行而系统地变大或变小(若|r|<0.25,则可以认为零件的尺寸不随生产过程的进行而系统地
变大或变小).
(2)一天内抽检零件中,如果出现了尺寸在(![]() ﹣3s,
﹣3s,![]() +3s)之外的零件,就认为这条生产线在这一天
+3s)之外的零件,就认为这条生产线在这一天
的生产过程可能出现了异常情况,需对当天的生产过程进行检查.
①从这一天抽检的结果看,是否需对当天的生产过程进行检查?
②在(![]() ﹣3s,
﹣3s,![]() +3s)之外的数据称为离群值,试剔除离群值,估计这条生产线当天生产的零件尺寸的
+3s)之外的数据称为离群值,试剔除离群值,估计这条生产线当天生产的零件尺寸的
均值与标准差.(精确到0.01)
附:样本(xi,yi)(i=1,2,…,n)的相关系数r=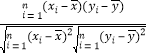 ,
,![]() ≈0.09.
≈0.09.