题目内容
【题目】已知函数f(x)= ![]() +x.
+x.
(1)若函数f(x)的图象在(1,f(1))处的切线经过点(0,﹣1),求a的值;
(2)是否存在负整数a,使函数f(x)的极大值为正值?若存在,求出所有负整数a的值;若不存在,请说明理由;
(3)设a>0,求证:函数f(x)既有极大值,又有极小值.
【答案】
(1)解:∵ ![]() ,f′(1)=1,f(1)=ae+1
,f′(1)=1,f(1)=ae+1
∴函数f(x)在(1,f(1))处的切线方程为:y﹣(ae+1)=x﹣1,又直线过点(0,﹣1)
∴﹣1﹣(ae+1)=﹣1,解得:a=﹣ ![]()
(2)解:若a<0,∵ ![]() (x≠0),
(x≠0),
当x∈(﹣∞,0)时,f′(x)>0恒成立,函数在(﹣∞,0)上无极值;
当x∈(0,1)时,f′(x)>0恒成立,函数在(0,1)上无极值;
在x∈(1,+∞)时,令H(x)=aex(x﹣1)+x2,则H′(x)=(aex+2)x,
∵x∈(1,+∞),∴ex∈(e,+∞,)∵a为负整数∴a≤﹣1,∴aex≤ae≤﹣e
∴aex+2<0,∴H′(x)<0,∴H(x)在(1,+∞)上单调减,
又H(1)=1>0,H(2)=ae2+4≤﹣e2+4<0∴x0∈(1,2),使得H(x0)=0
且1<x<x0时,H′(x)>0,即f′(x)>0;x>x0时,H′(x)<0,即f′(x)<0;
∴f(x)在x0处取得极大值 ![]() (*)
(*)
又H(x0)=aex0(x0﹣1)+x02=0,∴ ![]() 代入(*)得:
代入(*)得:
![]() ,∴不存在负整数a满足条件
,∴不存在负整数a满足条件
(3)解:设g(x)=aex(x﹣1)+x2,则g′(x)=(aex+2)x,
因为a>0,所以,当x>0时,g′(x)>0,g(x)单调递增;
当x<0时,g′(x)<0,g(x)单调递减;故g(x)至多两个零点.
又g(0)=﹣a<0,g(1)=1>0,所以存在x1∈(0,1),使g(x1)=0
再由g(x)在(0,+∞)上单调递增知,
当x∈(0,x1)时,g(x)<0,故f′(x)= ![]() ,f(x)单调递减;
,f(x)单调递减;
当x∈(x2,+∞)时,g(x)>0,故故f′(x)= ![]() ,f(x)单调递增;
,f(x)单调递增;
所以函数f(x)在x1处取得极小值.
当x<0时,ex<1,且x﹣1<0,
所以g(x)=aex(x﹣1)+x2>a(x﹣1)+x2=x2+ax﹣a,
函数y=x2+ax﹣a是关于x的二次函数,必存在负实数t,使g(t)>0,又g(0)=﹣a<0,
故在(t,0)上存在x2,使g(x2)=0,
再由g(x)在(﹣∞,0)上单调递减知,
当x∈(﹣∞,x2)时,g(x)>0,故f′(x)= ![]() ,f(x)单调递增;
,f(x)单调递增;
当x∈(x2,0)时,g(x)<0,故f′(x)= ![]() ,f(x)单调递减;
,f(x)单调递减;
所以函数f(x)在x2处取得极大值.
综上,函数f(x)既有极大值,又有极小值
【解析】(1)第一步确定切点;第二步求斜率,即求曲线上该点的导数;第三步利用点斜式求出直线方程.(2)根据可导函数极值的定义,找到极值点,求出极值,当极大值为正数时,从而判定负整数是否存在;(3)利用单调性与极值的关系,求证:既存在极大值,有存在极小值.
【考点精析】利用函数的极值与导数对题目进行判断即可得到答案,需要熟知求函数![]() 的极值的方法是:(1)如果在
的极值的方法是:(1)如果在![]() 附近的左侧
附近的左侧![]() ,右侧
,右侧![]() ,那么
,那么![]() 是极大值(2)如果在
是极大值(2)如果在![]() 附近的左侧
附近的左侧![]() ,右侧
,右侧![]() ,那么
,那么![]() 是极小值.
是极小值.

【题目】为了监控某种零件的一条生产线的生产过程,检验员每隔30 min从该生产线上随机抽取一个零件,并测量其尺寸(单位:cm).下面是检验员在一天内依次抽取的16个零件的尺寸:
抽取顺序 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
零件尺寸 | 9.95 | 10.12 | 9.96 | 9.96 | 10.01 | 9.92 | 9.98 | 10.04 |
抽取次序 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 |
零件尺寸 | 10.26 | 9.91 | 10.13 | 10.02 | 9.22 | 10.04 | 10.05 | 9.95 |
经计算得![]() =
=![]() xi=9.97,s=
xi=9.97,s=![]() =
=![]() ≈0.212,
≈0.212,![]() ≈18.439,
≈18.439,![]() (xi﹣
(xi﹣![]() )(i﹣8.5)=﹣2.78,
)(i﹣8.5)=﹣2.78,
其中xi为抽取的第i个零件的尺寸,i=1,2,…,16.
(1)求(xi,i)(i=1,2,…,16)的相关系数r,并回答是否可以认为这一天生产的零件尺寸不随生产
过程的进行而系统地变大或变小(若|r|<0.25,则可以认为零件的尺寸不随生产过程的进行而系统地
变大或变小).
(2)一天内抽检零件中,如果出现了尺寸在(![]() ﹣3s,
﹣3s,![]() +3s)之外的零件,就认为这条生产线在这一天
+3s)之外的零件,就认为这条生产线在这一天
的生产过程可能出现了异常情况,需对当天的生产过程进行检查.
①从这一天抽检的结果看,是否需对当天的生产过程进行检查?
②在(![]() ﹣3s,
﹣3s,![]() +3s)之外的数据称为离群值,试剔除离群值,估计这条生产线当天生产的零件尺寸的
+3s)之外的数据称为离群值,试剔除离群值,估计这条生产线当天生产的零件尺寸的
均值与标准差.(精确到0.01)
附:样本(xi,yi)(i=1,2,…,n)的相关系数r=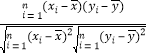 ,
,![]() ≈0.09.
≈0.09.
【题目】某校高一年级3个班有10名学生在全国英语能力大赛中获奖,学生来源人数如表:
班别 | 高一(1)班 | 高一(2)班 | 高一(3)班 |
人数 | 3 | 6 | 1 |
若要求从10位同学中选出两位同学介绍学习经验,设其中来自高一(1)班的人数为ξ,求随机变量ξ的分布列及数学期望E(ξ).
