题目内容
【题目】如图,![]() 是半圆
是半圆![]() 的直径,平面
的直径,平面![]() 与半圆
与半圆![]() 所在的平面垂直,
所在的平面垂直,![]() ,
,![]() ,
, ![]() ,
,![]() 是半圆
是半圆![]() 上不同于
上不同于![]() ,
,![]() 的点,四边形
的点,四边形![]() 是矩形.
是矩形.
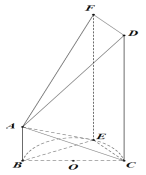
(Ⅰ)若![]() ,证明:
,证明:![]() 平面
平面![]() ;
;
(Ⅱ)若![]() ,求三棱锥
,求三棱锥![]() 体积的最大值.
体积的最大值.
【答案】(Ⅰ)详见解析;(Ⅱ)![]() .
.
【解析】
(Ⅰ)先证明![]() 平面
平面![]() ,从而可得
,从而可得![]() ,过点
,过点![]() 作
作![]() ,垂足为
,垂足为![]() ,可得到
,可得到![]() ,由勾股定理可得
,由勾股定理可得![]() ,从而可证.
,从而可证.
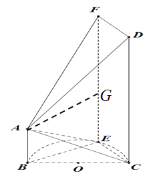
(Ⅱ)过点![]() 作
作![]() ,垂足为
,垂足为![]() ,可得
,可得![]() ,由
,由![]() ,作
,作![]() 于
于![]() ,由(Ⅰ)知
,由(Ⅰ)知![]() 平面
平面![]() ,则
,则![]() 是三棱锥
是三棱锥![]() 的高,当
的高,当![]() 最大,即点
最大,即点![]() 与点
与点![]() 重合时,三棱锥
重合时,三棱锥![]() 的体积最大,从而可求出答案.
的体积最大,从而可求出答案.
(Ⅰ)∵平面![]() 与半圆
与半圆![]() 所在的平面垂直,
所在的平面垂直,
∴平面![]() 平面
平面![]() ,
,
又平面![]() 平面
平面![]() ,
,![]() ,
,
∴![]() 平面
平面![]()
∵![]() 平面
平面![]() ,
,
∴![]() ,
,
∵![]() 是半圆
是半圆![]() 上一点,
上一点,
∴![]() ,
,
又![]() ,
,
∴![]() 平面
平面![]() ,
,
∵![]() 平面
平面![]() ,
,
∴![]()
∵四边形![]() 是矩形,
是矩形,
∴![]() ,
,
由![]() ,
,![]() ,
,![]() ,过点
,过点![]() 作
作![]() ,垂足为
,垂足为![]() ,
,
则![]() ,
,![]() ,
,
![]() ,
,![]() ,
,
∴![]() ,
,
∴![]()
又![]() ,
,
∴![]() 平面
平面![]()
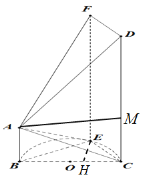
(Ⅱ)在平面![]() 内,作
内,作![]() 于
于![]() ,由(Ⅰ)知
,由(Ⅰ)知![]() 平面
平面![]() ,
,
则![]() 是三棱锥
是三棱锥![]() 的高,
的高,
∴当![]() 最大,即点
最大,即点![]() 与点
与点![]() 重合时,三棱锥
重合时,三棱锥![]() 的体积最大,此时
的体积最大,此时![]()
∵![]() ,
,![]() ,过点
,过点![]() 作
作![]() ,垂足为
,垂足为![]() ,
,
则![]() ,
,![]() ,
,
∴![]() ,
,
∴三棱锥![]() 体积的最大值为
体积的最大值为![]() .
.

【题目】某工厂的![]() ,
,![]() ,
,![]() 三个不同车间生产同一产品的数量(单位:件)如下表所示.质检人员用分层抽样的方法从这些产品中共抽取6件样品进行检测:
三个不同车间生产同一产品的数量(单位:件)如下表所示.质检人员用分层抽样的方法从这些产品中共抽取6件样品进行检测:
车间 |
|
|
|
数量 | 50 | 150 | 100 |
(1)求这6件样品中来自![]() ,
,![]() ,
,![]() 各车间产品的数量;
各车间产品的数量;
(2)若在这6件样品中随机抽取2件进行进一步检测,求这2件产品来自相同车间的概率.
【题目】针对国家提出的延迟退休方案,某机构进行了网上调查,所有参与调查的人中,持“支持”、“保留”和“不支持”态度的人数如下表所示:
| 支持 | 保留 | 不支持 |
|
|
|
|
|
|
|
|
(1)在所有参与调查的人中,用分层抽样的方法抽取![]() 个人,已知从持“不支持”态度的人中抽取了
个人,已知从持“不支持”态度的人中抽取了![]() 人,求
人,求![]() 的值;
的值;
(2)在持“不支持”态度的人中,用分层抽样的方法抽取![]() 人看成一个总体,从这
人看成一个总体,从这![]() 人中任意选取
人中任意选取![]() 人,求至少有一人年龄在
人,求至少有一人年龄在![]() 岁以下的概率.
岁以下的概率.
(3)在接受调查的人中,有![]() 人给这项活动打出的分数如下:
人给这项活动打出的分数如下: ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,把这
,把这![]() 个人打出的分数看作一个总体,从中任取一个数,求该数与总体平均数之差的绝对值超过
个人打出的分数看作一个总体,从中任取一个数,求该数与总体平均数之差的绝对值超过![]() 概率.
概率.

