题目内容
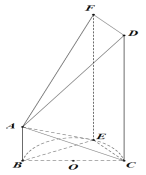
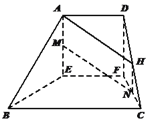
【题目】在如图如示的多面体中,平面![]() 平面
平面![]() ,四边形
,四边形![]() 是边长为
是边长为![]() 的正方形,
的正方形, ![]() ∥
∥![]() ,且
,且![]() .
.
(1)若![]() 分别是
分别是![]() 中点,求证:
中点,求证: ![]() ∥平面
∥平面![]()
(2)求此多面体![]() 的体积
的体积


【答案】(1)见解析(2)![]()
【解析】试题分析:
(1)在平面![]() 中,作
中,作![]() 交DC于
交DC于![]() 连接
连接![]() ,根据条件可得四边形
,根据条件可得四边形![]() 是平行四边形,于是
是平行四边形,于是![]() ∥
∥![]() ,由线面平行的判定定理可得结论成立.(2)结合图形将多面体
,由线面平行的判定定理可得结论成立.(2)结合图形将多面体![]() 的体积分为
的体积分为![]() 两部分求解,由题意分别求得两个椎体的高即可.
两部分求解,由题意分别求得两个椎体的高即可.
试题解析:
(1)证明:在平面![]() 中,作
中,作![]() 交DC于
交DC于![]() 连接
连接![]() .
.
![]()
![]() 是
是![]() 中点,且
中点,且![]() 是正方形,
是正方形,
![]() ∥
∥![]() ,
, ![]() ,
,
又![]() ∥
∥![]() ,
, ![]() ,
,
![]() ,
,
![]() 四边形
四边形![]() 是平行四边形,
是平行四边形,
![]() ∥
∥![]() ,
,
又![]() 平面
平面![]() ,
, ![]()
![]() 平面
平面![]() ,
,
![]() ∥平面
∥平面![]() .
.
(2)解:如图,连BD,BF,过F作FG⊥EF,交BC于点G.
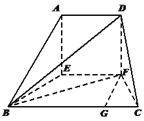
![]() 四边形BEFC是等腰梯形,
四边形BEFC是等腰梯形,
![]() .
.
![]() 平面
平面![]()
![]() 平面
平面![]() ,平面
,平面![]()
![]() 平面
平面![]() ,FG⊥EF,DF⊥EF,
,FG⊥EF,DF⊥EF,
![]() 平面
平面![]() ,
, ![]()
![]() 平面
平面![]() .
.
![]() ,
,
![]() ,
,
故多面体![]() 的体积
的体积![]() .
.

练习册系列答案
相关题目