题目内容
【题目】M是正方体
的棱
的中点，给出下列四个命题：①过M点有且只有一条直线与直线
都相交；②过M点有且只有一条直线与直线都垂直；③过M点有且只有一个平面与直线都相交；④过M点有且只有一个平面与直线都平行；其中真命题是（ ）
A.②③④B.①③④C.①②④D.①②③
【答案】C
【解析】
利用反证法说明①正确,通过直接作平面说明②④正确，直接作平面说明③错误.
由题意得直线
与
是两条互相垂直的异面直线，点
不在这两异面直线中的任何一条上，
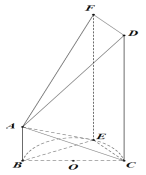
假设过点有两条直线与直线都相交，如图，
设交点分别为
,则
四点共面，从而直线共面，与与异面矛盾，因此假设不成立；显然过点多于两条直线与直线都相交也不成立，故过M点有且只有一条直线与直线
都相交，①正确．
过点作直线
分别与直线平行，如图，
因为直线异面，所以直线
必为相交直线，即可确定一个平面
，因为与直线都垂直的直线必垂直这个平面，而过点有且只有一条直线
与平面垂直，所以过M点有且只有一条直线与直线都垂直，故②正确．
因为点不在这两异面直线中的任何一条上，所以平面与直线都平行，根据作法知平面只有一个，所以过点有且只有一个平面与直线都平行，故④正确．
在平面过点作直线
（与不重合）,如图
则，确定的平面都与直线都相交，由有无数条，所以过M点有无数个平面与直线都相交，故③不正确．
故选：C
练习册系列答案
阅读快车系列答案
相关题目
