题目内容
【题目】已知0＜x＜1，0＜y＜1， 求证 
+ 
+ 
+ 
≥2 
，并求使等号成立的条件．
【答案】证明：∵0＜x＜1，0＜y＜1，设P（x，y），A（1，0），B（1，1），C（0，1），如图： 则|PO|= 
，|PA|= 
，|PB|= 
，|PC|= 
，
∵|PO|+|PB|≥|BO|= 
，|PA|+|PC|≥|AC|=
∴|PO|+|PB|+|PA|+|PC|≥2 （当且仅当点P为正方形的对角线AC与OB的交点是取等号），
即x=y= 
时取等号．
∴ + + + 
．
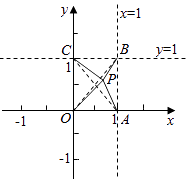
【解析】依题意，作图如下，利用两点间的距离公式可知|PO|= 
，|PA|= 
，|PB|= 
，|PC|= 
，利用三角不等式可证|PO|+|PB|+|PA|+|PC|≥2 
【考点精析】解答此题的关键在于理解二维形式的柯西不等式的相关知识，掌握二维形式的柯西不等式：
当且仅当
时，等号成立．
练习册系列答案
相关题目
【题目】某产品的广告费用x与销售额y的统计数据如表：
广告费用x（万元） | 1 | 2 | 4 | 5 |
销售额y（万元） | 6 | 14 | 28 | 32 |
根据上表中的数据可以求得线性回归方程 
= 
x+ 
中的 为6.6，据此模型预报广告费用为10万元时销售额为（ ）
A.66.2万元
B.66.4万元
C.66.8万元
D.67.6万元
