题目内容
【题目】据调查,某地区有300万从事传统农业的农民,人均年收入6000元,为了增加农民的收入,当地政府积极引进资本,建立各种加工企业,对当地的农产品进行深加工,同时吸收当地部分农民进入加工企业工作,据估计,如果有![]() 万人进企业工作,那么剩下从事传统农业的农民的人均年收入有望提高
万人进企业工作,那么剩下从事传统农业的农民的人均年收入有望提高![]() ,而进入企业工作的农民的人均年收入为
,而进入企业工作的农民的人均年收入为![]() 元.
元.
(1)在建立加工企业后,多少农民进入企业工作,能够使剩下从事传统农业农民的总收入最大,并求出最大值;
(2)为了保证传统农业的顺利进行,限制农民加入加工企业的人数不能超过总人数的![]() ,当地政府如何引导农民,即
,当地政府如何引导农民,即![]() 取何值时,能使300万农民的年总收入最大.
取何值时,能使300万农民的年总收入最大.
【答案】(1)见解析;(2)见解析
【解析】
![]() 根据题意建立函数关系结合二次函数的单调性的性质进行求解即可;
根据题意建立函数关系结合二次函数的单调性的性质进行求解即可;![]() 根据条件设300万农民的年总收入为
根据条件设300万农民的年总收入为![]() ,建立函数关系,利用一元二次函数的性质进行求解
,建立函数关系,利用一元二次函数的性质进行求解
![]() 由题意如果有
由题意如果有![]() 万人进企业工作,设从事传统农业的所有农民的总收入为y,
万人进企业工作,设从事传统农业的所有农民的总收入为y,
则![]() ,
,![]() ,
,
对称轴为![]() ,抛物线开口向下,即当
,抛物线开口向下,即当![]() 时,y取得最大值为
时,y取得最大值为![]() 万元
万元![]() .
.
即由100万人进企业工作,能够使剩下从事传统农业的所有农民的总收入最大,最大为2400000万元.
![]() 设300万农民的总收入为
设300万农民的总收入为![]() ,
,![]() ,
,
则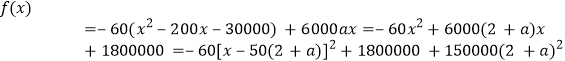 ,
,
对称轴为![]() ,
,
![]() 当
当![]() 时,
时,![]() ,当
,当![]() 时,
时,![]() 取得最大值,
取得最大值,
![]() 当
当![]() 时,
时,![]() ,当
,当![]() 时,
时,![]() 取得最大值.
取得最大值.

 新课标快乐提优暑假作业陕西旅游出版社系列答案
新课标快乐提优暑假作业陕西旅游出版社系列答案【题目】一只药用昆虫的产卵数![]() 与一定范围内与温度
与一定范围内与温度![]() 有关, 现收集了该种药用昆虫的6组观测数据如下表:
有关, 现收集了该种药用昆虫的6组观测数据如下表:
温度 | 21 | 23 | 24 | 27 | 29 | 32 |
产卵数 | 6 | 11 | 20 | 27 | 57 | 77 |
(1)若用线性回归模型,求![]() 关于
关于![]() 的回归方程
的回归方程![]() =
=![]() x+
x+![]() (精确到0.1);
(精确到0.1);
(2)若用非线性回归模型求![]() 关
关![]() 的回归方程为
的回归方程为![]()
![]() 且相关指数
且相关指数![]()
( i )试与 (1)中的线性回归模型相比,用![]() 说明哪种模型的拟合效果更好.
说明哪种模型的拟合效果更好.
( ii )用拟合效果好的模型预测温度为![]() 时该种药用昆虫的产卵数(结果取整数).
时该种药用昆虫的产卵数(结果取整数).
附:一组数据(x1,y1), (x2,y2), ...,(xn,yn), 其回归直线![]() =
=![]() x+
x+![]() 的斜率和截距的最小二乘估计为
的斜率和截距的最小二乘估计为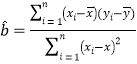 ,
,![]() ,相关指数
,相关指数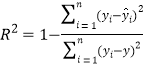 .
.
![]()
![]()
![]()
![]() 。
。
